Find the moment of inertia of a thin uniform rod about an axis perpendicular to its length and passing through a point which is at a distance of $\frac{1}{3}$ from one end. Also find radius of gyration about that axis.

Video Solution

Text Solution

Verified by Experts

(i) Let $P$ be the point at a distance $\frac{l}{3}$ from one end. It is a distance of $(\frac{l}{2} - \frac{l}{3}) = \frac{l}{6}$ from the centre as shown in the figure.

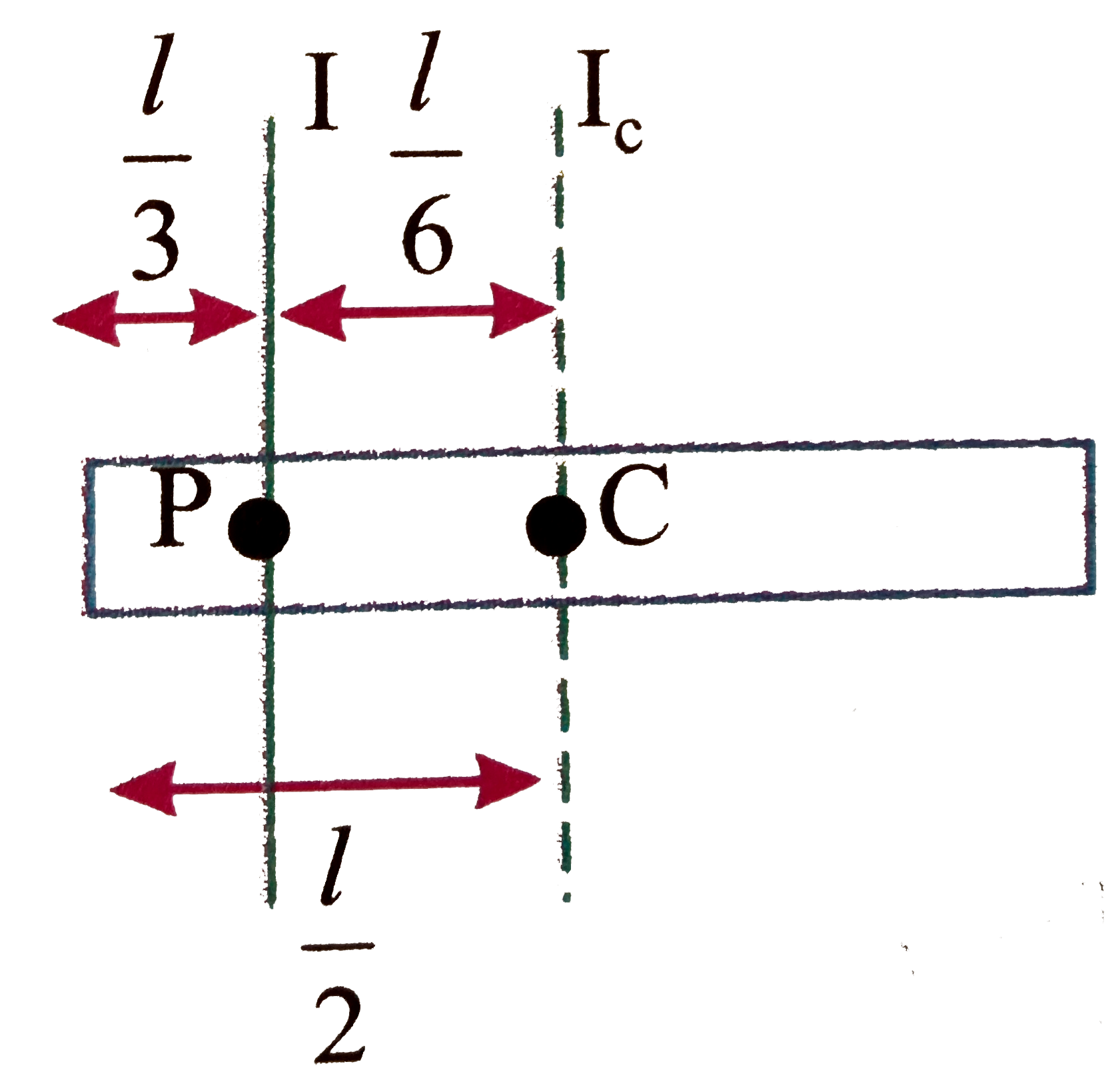
By parallel axes theoram $I = I_{C} = M r^{2}$
$= \frac{M I^{2}}{12} + M {(\frac{l}{6})}^{2} = \frac{M l^{2}}{9}$
ii. The radius of gyration, $K = \sqrt{\frac{I}{M}} = \sqrt{\frac{M I^{2}}{9 M}} = \frac{l}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of gyration of rod of length $L$ and mass $M$ about an axis perpendicular to its length and passing through a point at a distance $L / 3$ from one of its ends is
A $\frac{\sqrt{7}}{6} L$
B $\frac{L^{2}}{9}$
C $\frac{L}{3}$
D $\frac{\sqrt{5}}{2} L$
Question 2 - Select One
The moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
A $\frac{m l^{2}}{12}$
B $\frac{7}{48} m l^{2}$
C $\frac{13}{48} m l^{2}$
D $\frac{19}{48} m l^{2}$
Question 3 - Select One
If $I_{1}$ is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mas and $I_{2}$ is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
A $\frac{l_{1}}{l_{2}} = \frac{3}{π^{2}}$
B $\frac{l_{1}}{l_{2}} = \frac{2}{π^{2}}$
C $\frac{l_{1}}{l_{2}} = \frac{π^{2}}{2}$
D $\frac{l_{1}}{l_{2}} = \frac{π^{2}}{3}$

Recommended Questions

Home
Ask Doubt
Profile