Three identicle particle each of mass 1kg are placed with their centres on a straight line. Their centres are marked A,BandC respectively. The distance of centre of mass of the system from A is.
AB+AC2
AB+BC2
AC−AB3
AB+AC3
The correct Answer is:D
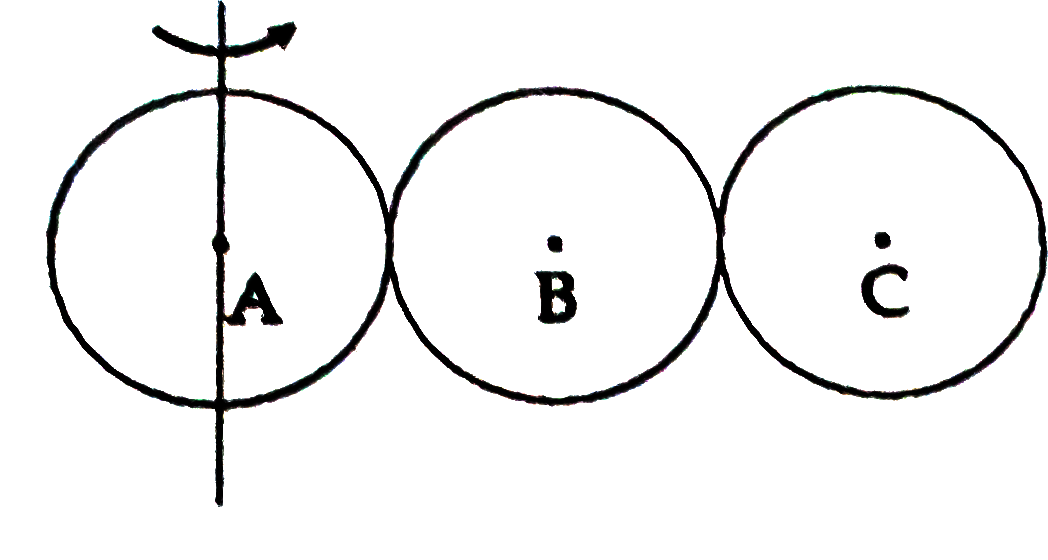
xcm=(x1+x2+x3)mm+m+m
=x1+x2+x33
=0+AB+AC2.
Topper's Solved these Questions
Similar Questions
Three identical particles each of same mass are placed touching each other with their centres on a straight line.Their centres are at A,B,and C respectively.Then distance of centre of mass of the system from A is
View SolutionFour identical bodies each of mass 1 kg are placed touching to each other with centres on a straight line. If their centres are marked A, B, C and D respectively, then the distance of centre of mass of the system from B will be

View Solution
Knowledge Check
The distance of centre of mass from O is
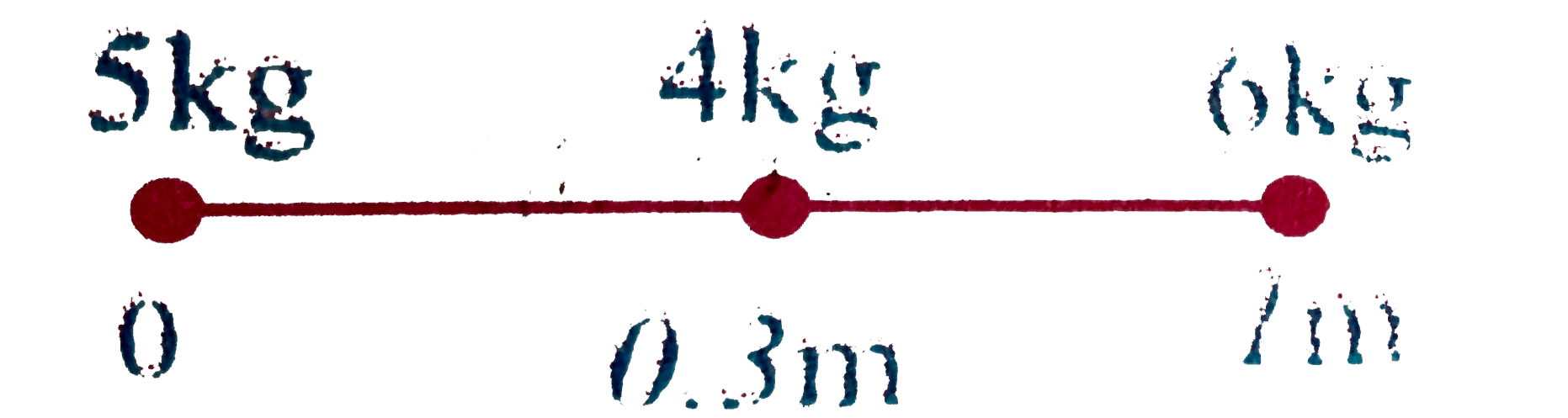 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48mThree identicle particle each of mass 1kg are placed with their centres on a straight line. Their centres are marked A,BandC respectively. The distance of centre of mass of the system from A is.
AKL+KM+LM3BKL+KM3CKL+LM3DKM+LM3The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particles
Three identical spheres, each of mass 1 kg are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked P, Q, R respectively, the distance of centre of mass of the system from P (origin) is
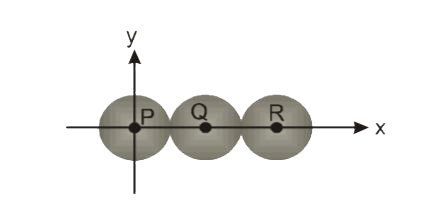
View SolutionQuestions on centre of mass of system of particle and bodies
View SolutionThree bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is

View SolutionThree identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
View SolutionThree particles each of mass m are arranged at the corners of an equililateral triangle of side L. If one of masses is doubled. The shift in the centre of mass of the system
View Solution
