Question

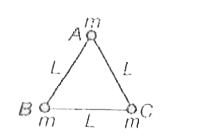
Three particles each of mass $m$ are arranged at the corners of an equililateral triangle of side $L$. If one of masses is doubled. The shift in the centre of mass of the system

Options

A. `L/(sqrt(3))`
B. `L/(4sqrt(3))`
C. `(sqrt(3)L)/4`
D. `L/(2sqrt(3))`

Answer

B

Explanation

To solve the problem of finding the shift in the center of mass when one of the masses at the corners of an equilateral triangle is doubled, we can follow these steps:

Step 1: Understand the Initial Configuration
We have three particles, each of mass `m`, located at the corners of an equilateral triangle with side length `L`. Let’s denote the positions of the particles as follows:
- Particle A at (0, 0)
- Particle B at (L, 0)
- Particle C at \((\frac{L}{2}, \frac{L\sqrt{3}}{2})\)

Step 2: Calculate the Initial Center of Mass
The center of mass (CM) of a system of particles is given by the formula:
\( \text{CM} = \frac{1}{M} \sum m_i \vec{r_i} \)
where \(M\) is the total mass and \(\vec{r_i}\) is the position vector of each mass.

The total mass \(M\) of the system is:
\( M = m + m + m = 3m \)

Now, we calculate the coordinates of the center of mass:
\( x_{CM} = \frac{1}{3m} \left( m \cdot 0 + m \cdot L + m \cdot \frac{L}{2} \right) = \frac{1}{3} \left( 0 + L + \frac{L}{2} \right) = \frac{1}{3} \left( \frac{3L}{2} \right) = \frac{L}{2} \)

\( y_{CM} = \frac{1}{3m} \left( m \cdot 0 + m \cdot 0 + m \cdot \frac{L\sqrt{3}}{2} \right) = \frac{1}{3} \left( 0 + 0 + \frac{L\sqrt{3}}{2} \right) = \frac{L\sqrt{3}}{6} \)

Thus, the initial center of mass is at:
\( \text{CM}_{initial} = \left( \frac{L}{2}, \frac{L\sqrt{3}}{6} \right) \)

Step 3: Modify the Mass of One Particle
Now, let’s double the mass of particle A. The new mass configuration is:
- Particle A: \(2m\)
- Particle B: \(m\)
- Particle C: \(m\)

Step 4: Calculate the New Center of Mass
The new total mass \(M'\) is:
\( M' = 2m + m + m = 4m \)

Now, we calculate the new coordinates of the center of mass:
\( x_{CM}' = \frac{1}{4m} \left( 2m \cdot 0 + m \cdot L + m \cdot \frac{L}{2} \right) = \frac{1}{4} \left( 0 + L + \frac{L}{2} \right) = \frac{1}{4} \left( \frac{3L}{2} \right) = \frac{3L}{8} \)

\( y_{CM}' = \frac{1}{4m} \left( 2m \cdot 0 + m \cdot 0 + m \cdot \frac{L\sqrt{3}}{2} \right) = \frac{1}{4} \left( 0 + 0 + \frac{L\sqrt{3}}{2} \right) = \frac{L\sqrt{3}}{8} \)

Thus, the new center of mass is at:
\( \text{CM}_{new} = \left( \frac{3L}{8}, \frac{L\sqrt{3}}{8} \right) \)

Step 5: Calculate the Shift in Center of Mass
The shift in the center of mass can be calculated as:
\( \Delta x = x_{CM}' - x_{CM} = \frac{3L}{8} - \frac{L}{2} = \frac{3L}{8} - \frac{4L}{8} = -\frac{L}{8} \)

\( \Delta y = y_{CM}' - y_{CM} = \frac{L\sqrt{3}}{8} - \frac{L\sqrt{3}}{6} \)
To find a common denominator (24):
\( \Delta y = \frac{3L\sqrt{3}}{24} - \frac{4L\sqrt{3}}{24} = -\frac{L\sqrt{3}}{24} \)

Final Result
The shift in the center of mass is:
\( \Delta \text{CM} = \left( -\frac{L}{8}, -\frac{L\sqrt{3}}{24} \right) \)