Three liquids of the same amount are mixed. The specific heats of these liquids are s1,s2ands3 and their initial temperature are θ1,θ2andθ3, respectively. Find out the final temperature of the mixture.Solution in Bengali
Let the final temperature of the mixture be θ and the mass of each liquid be m.
∴ Heat absorbed by the 1st liquid, H1=ms1(θ−θ1)
Heat absorbed by the 2nd liquid, H2=ms2(θ−θ2)
Heat absorbed by the 3rd liquid, H3=ms3(θ−θ3)
Since no heat is supplied from outside,
∴ H1+H2+H3=0 ...(1)
[any one or two of H1,H2,H3 must be negative, implying heat lost, then equation (1) means, heat gained = heat lost]
∴ ms1(θ−θ1)+ms2(θ−θ2)+ms3(θ−θ3)=0
or, θ(s1+s2+s3)=s1θ1+s2θ2+s3θ3
or, θ(s1+s2+s3)=s1θ1+s2θ2+s3θ3
or, θ=s1θ1+s2θ2+s3θ3s1+s2+s3
Topper's Solved these Questions
- CALORIMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - CALORIMETRYEXERCISE - Section Related Questions
1 Videos
- CALORIMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - CALORIMETRYEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
15 Videos
- CIRCULAR MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - CBSE SCANNER
11 Videos
Similar Questions
'Specific heat of iron is 0.106 cal.g−1.∘C−1'- what do you mean by this statement?
View SolutionEqual masses of milk and water are taken in two identical kettles and heated by the same source. The ratio of rise of temperature of milk is found to be higher than that of water. Explain.
View SolutionDerive an expression for the acceleration of a body of mass m moving with a uniform speed v in circular path of radius r.
View SolutionIf sinθ1+sinθ2+sinθ3, then find the value of cosθ1+cosθ2+cosθ3.
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
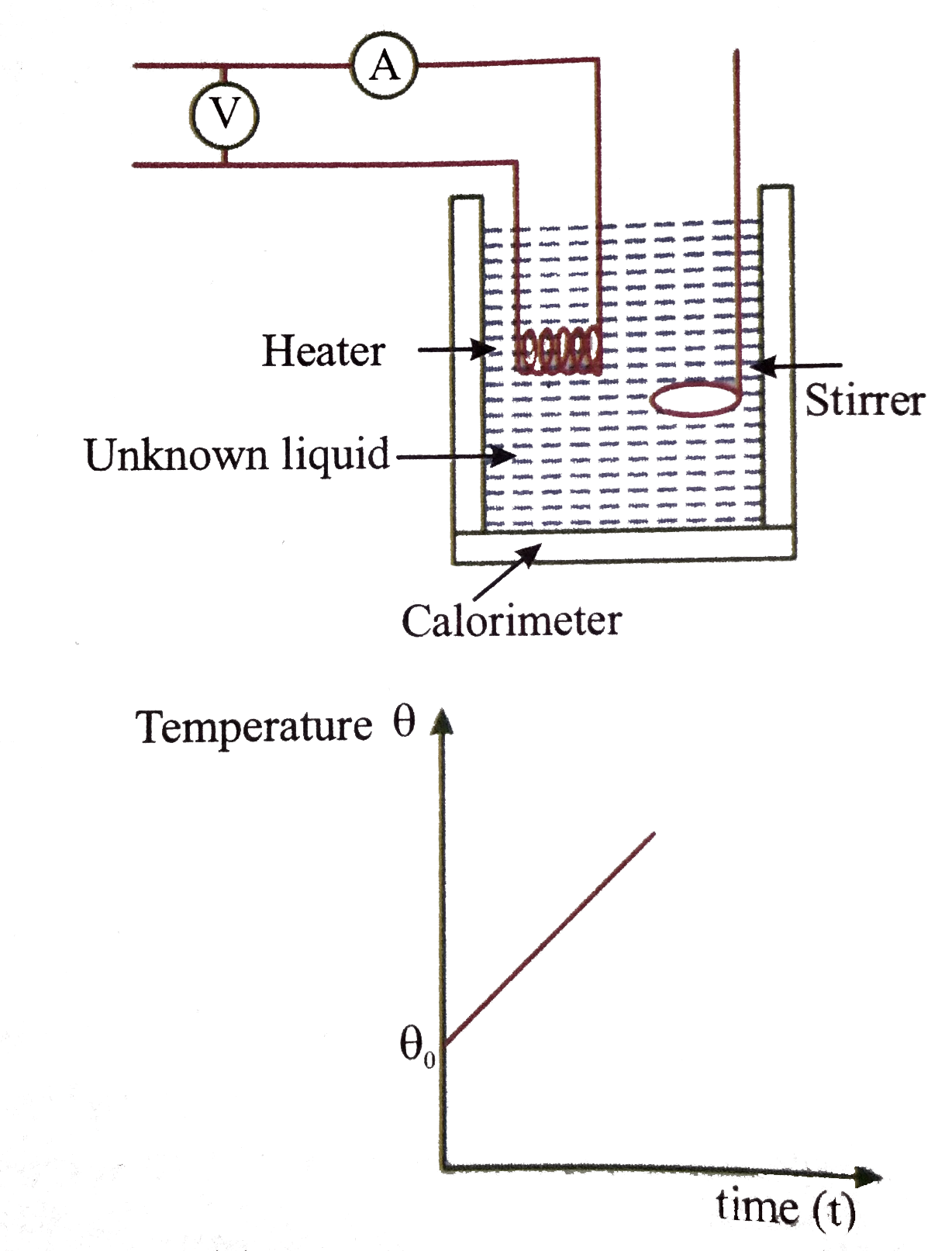
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is varepsilon
Now the corrected final temperature is taken as θf=θf+ɛ
In this experiment voltage across the heater is 100.0V and current is 10.0A, and heater was switched on for t=700.0sec. Initially all elements were at room temperature θ∘=10.0∘C and final temperature was measured as θf=73.0∘C.
Mass of empty calorimeter ws 1.0kg and the combined mass of calorimeter + liquid is 3.0kg. The specific heat capacity of the calorimeter =3.0×103J/kg∘C. The falls in temperature 350 second after switching off the heater was 7.0∘C. Find the specific heat capacity of the unknown liquid in proper significant figures.
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is m1. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be m2. So the mass of liquid is (m2−m1). Initially both were at room temperature (θ0).
Now a heater is immeresed in if for time interval t. The voltage drop across the heater is V and current passing through it is I. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After tsec, heater was switched off, and final temperature is θr. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter (VI)t=(m2−m1)S1(θf−θ0)+m1Sc(θf−θ0)
The specific heat of the liquid S1=(VI)tθf−θ0−m1Sc(m2−m1)
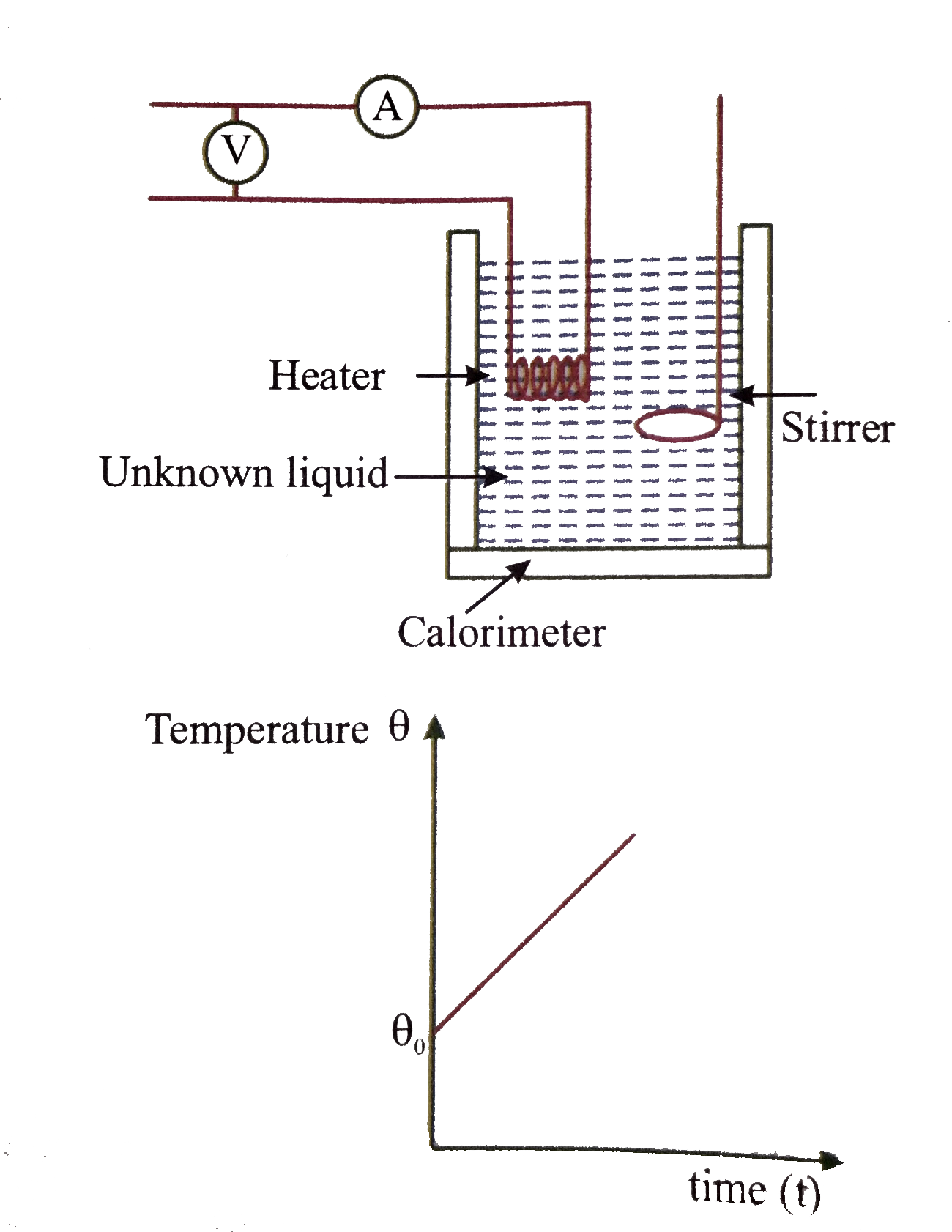
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for tsec, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured t/2sec. after switching off. Let the fall in temperature during this time is ɛ
Now the corrected final temperature is taken as θf=θf+ɛ
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in Sl. Use the date mentioned below.
m1→, Sl→0, m2=1.00kg,
V=10.0V, I=10.0A,
t=1.00×102sec, θ0=15∘C,
Corrected θ1=65∘C
View SolutionIf three different liquid of different masses specific heats and temperature are mixed with each other and then what is the temperature mixture at thermal equilibrium. m_(1),s_(1),T_(1) rarr specification for liquid m_(2),s_(2),T_(2)rarr specification for liquid. m_(3),s_(3),T_(3)rarr specification for liquid.
View SolutionEqual masses of three liquids are thoroughly mixed. The specific heat capacities of the liquids ar s1,s2 and s3 and their temperatures t1,t2 and t3 respectively. Find the temperature of the mixture.
View SolutionThe specific heat capacities of n liquid are s_(1),s_(2),s_(3) ,…….. s_(n) respectively and their respective temperatures t_(1),t_(2), t_(3) ,…….t_(n) . Equal masses of the liquids are mixed together. Find the temperature of the mixture.
View SolutionIf the loss in graviational potential energy to falling the sphere by h height and heat loss to surrounding at constant rate H are also taken to account the energy equation will modify to (A) m_(1) s_(1) (theta_(1)-theta) + (m_(1)gh)/(J) = m_(2) s_(2) (theta - theta_(2)) + m_(3) s_(3) (theta - theta_(2)) - H t (B) m_(1)s_(1) (theta_(1) -theta) - (m_(1)gh)/(J) = m_(2)s_(2)(theta -theta_(2)) + m_(3) s_(3) (theta -theta_(2)) + Ht (C) m_(1)s_(1) (theta_(1) -theta) + (m_(1)gh)/(J) = m_(2) s_(2) (theta - theta_(2)) + m_(3) s_(3) (theta -theta_(2)) + Ht (D) m_(1) s_(1) (theta_(1)-theta)-(m_(1)gh)/(J)=m_(2)s_(2)(theta-theta_(2)) +m_(3)s_(3)(theta-theta_(2))-Ht .
View Solutionयदि tan(θ1+θ2)=tanθ1+tanθ21−tanθ1tanθ2,θ1 व θ2 न्यूनकोण है तब θ1+θ2 का मान ज्ञात कीजिए यदि tanθ1=12 व tanθ2=13
View SolutionLet z1,z2 and z3 be three points on |z|=1. If θ1,θ2 and θ3 be the arguments of z1,z2,z3 respectively, then cos(θ1−θ2)+cos(θ2−θ3)+cos(θ3−θ1)
View SolutionThree liquids of masses m_(1),m_(2) and m_(3) are mixed together. Their specific heats are s_(1), s_(2) and s_(3) , and they were at temperature t_(1),t_(2) and t_(3) respectively. Calculate the temperature of the mixture.
View SolutionTwo liquids of masses M_(1) , and M_(2) and specific heats S_(1) , and S_(2) , respectively are mixed. The specific heat of the mixtureis
View Solutionसम्मिश्र संख्या z=3+4i के मापांक तथा कोणांक ज्ञात कीजिये ।
View Solution
