Three liquids with masses m1,m2,m3 are throughly mixed. If their specific heats are c1,c2,c3 and their temperature T1,T2,T3, respectively, then the temperature of the mixture is
c1T1+c2T2+c3T3m1c1+m2c2+m3c3
m1c1T1+m2c2t2+m3c3T3m1c1+m2c2+m3c3
m1c1T1+m2c2T2+m3c3T3m1T1+m2T2+m3T3
m1T1+m2T2+m3T3c1T1+c2T2+c3T3
The correct Answer is:B
To find the final temperature of a mixture of three liquids with given masses, specific heats, and initial temperatures, we can follow these steps:
1. Identify the Parameters:
- Let the masses of the three liquids be m1,m2,m3.
- Let the specific heats of the three liquids be c1,c2,c3.
- Let the initial temperatures of the three liquids be T1,T2,T3.
2. Calculate the Total Heat Supplied:
- When the liquids are cooled down to 0°C, the heat lost by each liquid can be expressed as:
- For liquid 1: Q1=m1c1(T1−0)=m1c1T1
- For liquid 2: Q2=m2c2(T2−0)=m2c2T2
- For liquid 3: Q3=m3c3(T3−0)=m3c3T3
- Therefore, the total heat supplied by all three liquids when they cool down to 0°C is:
Qtotal=Q1+Q2+Q3=m1c1T1+m2c2T2+m3c3T3
3. Calculate the Heat Used to Raise the Temperature:
- After mixing, the temperature of the mixture rises from 0°C to a final temperature T.
- The heat used to raise the temperature of each liquid from 0°C to T can be expressed as:
- For liquid 1: Q′1=m1c1(T−0)=m1c1T
- For liquid 2: Q′2=m2c2(T−0)=m2c2T
- For liquid 3: Q′3=m3c3(T−0)=m3c3T
- Therefore, the total heat used to raise the temperature to T is:
Q′total=Q′1+Q′2+Q′3=m1c1T+m2c2T+m3c3T
4. Apply the Principle of Conservation of Energy:
- According to the law of calorimetry, the total heat lost by the liquids while cooling down to 0°C equals the total heat gained while raising the temperature to T:
m1c1T1+m2c2T2+m3c3T3=m1c1T+m2c2T+m3c3T
5. Rearrange the Equation:
- Rearranging the equation gives:
m1c1T1+m2c2T2+m3c3T3=T(m1c1+m2c2+m3c3)
6. Solve for the Final Temperature T:
- To find T, divide both sides by the total heat capacity:
T=m1c1T1+m2c2T2+m3c3T3m1c1+m2c2+m3c3
Final Answer:
The final temperature T of the mixture is given by:
T=m1c1T1+m2c2T2+m3c3T3m1c1+m2c2+m3c3
- Let the masses of the three liquids be m1,m2,m3.
- Let the specific heats of the three liquids be c1,c2,c3.
- Let the initial temperatures of the three liquids be T1,T2,T3.
- When the liquids are cooled down to 0°C, the heat lost by each liquid can be expressed as:
- For liquid 1: Q1=m1c1(T1−0)=m1c1T1
- For liquid 2: Q2=m2c2(T2−0)=m2c2T2
- For liquid 3: Q3=m3c3(T3−0)=m3c3T3
- Therefore, the total heat supplied by all three liquids when they cool down to 0°C is:
Qtotal=Q1+Q2+Q3=m1c1T1+m2c2T2+m3c3T3
- After mixing, the temperature of the mixture rises from 0°C to a final temperature T.
- The heat used to raise the temperature of each liquid from 0°C to T can be expressed as:
- For liquid 1: Q′1=m1c1(T−0)=m1c1T
- For liquid 2: Q′2=m2c2(T−0)=m2c2T
- For liquid 3: Q′3=m3c3(T−0)=m3c3T
- Therefore, the total heat used to raise the temperature to T is:
Q′total=Q′1+Q′2+Q′3=m1c1T+m2c2T+m3c3T
- According to the law of calorimetry, the total heat lost by the liquids while cooling down to 0°C equals the total heat gained while raising the temperature to T:
m1c1T1+m2c2T2+m3c3T3=m1c1T+m2c2T+m3c3T
- Rearranging the equation gives:
m1c1T1+m2c2T2+m3c3T3=T(m1c1+m2c2+m3c3)
- To find T, divide both sides by the total heat capacity:
T=m1c1T1+m2c2T2+m3c3T3m1c1+m2c2+m3c3
The final temperature T of the mixture is given by:
T=m1c1T1+m2c2T2+m3c3T3m1c1+m2c2+m3c3
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Equal volumes of three liquids of densities ρ1,ρ2 and ρ3, specific heat capacities c1,c2 and c3 and temperatures t1,t2 and t3, respectively are mixed together. What is the temperature of the mixture? Assume no changes in volume on mixing.
View SolutionThree liquids A, B and C having same sepcific heats have masses m,2m and 3m. Their temperaures are 0,20 and 3θ respectively. ltBrgt Q. What is the temperature of mixture, when Aand C all are mixed?
View SolutionThree liquids A, B and C having same sepcific heats have masses m,2m and 3m. Their temperaures are 'theta',2theta and 3θ respectively. Q. What is the temperature of mixture, when A and B are mixed?
View SolutionThree liquids A, B and C having same sepcific heats have masses m,2m and 3m. Their temperaures are 0,20 and 3θ respectively. ltBrgt Q. What is the temperature of mixture, when A and B mixed?
View SolutionA mass m1 of a substance of specific heat capacity c1 at temperature t1 is mixed with a mass m2 of other substance of specific heat capacity c2 at a lower temperature t2. Deduce the expression for the temperature t of the mixture. State the assumption made, if any.
View SolutionThree perfect gases at absolute temperature T1,T2,andT3 are mixed. The masses of molecules are n1,n2andn3 respectively. Assuming to loss of energy, the final temperature of the mixture is:
View Solution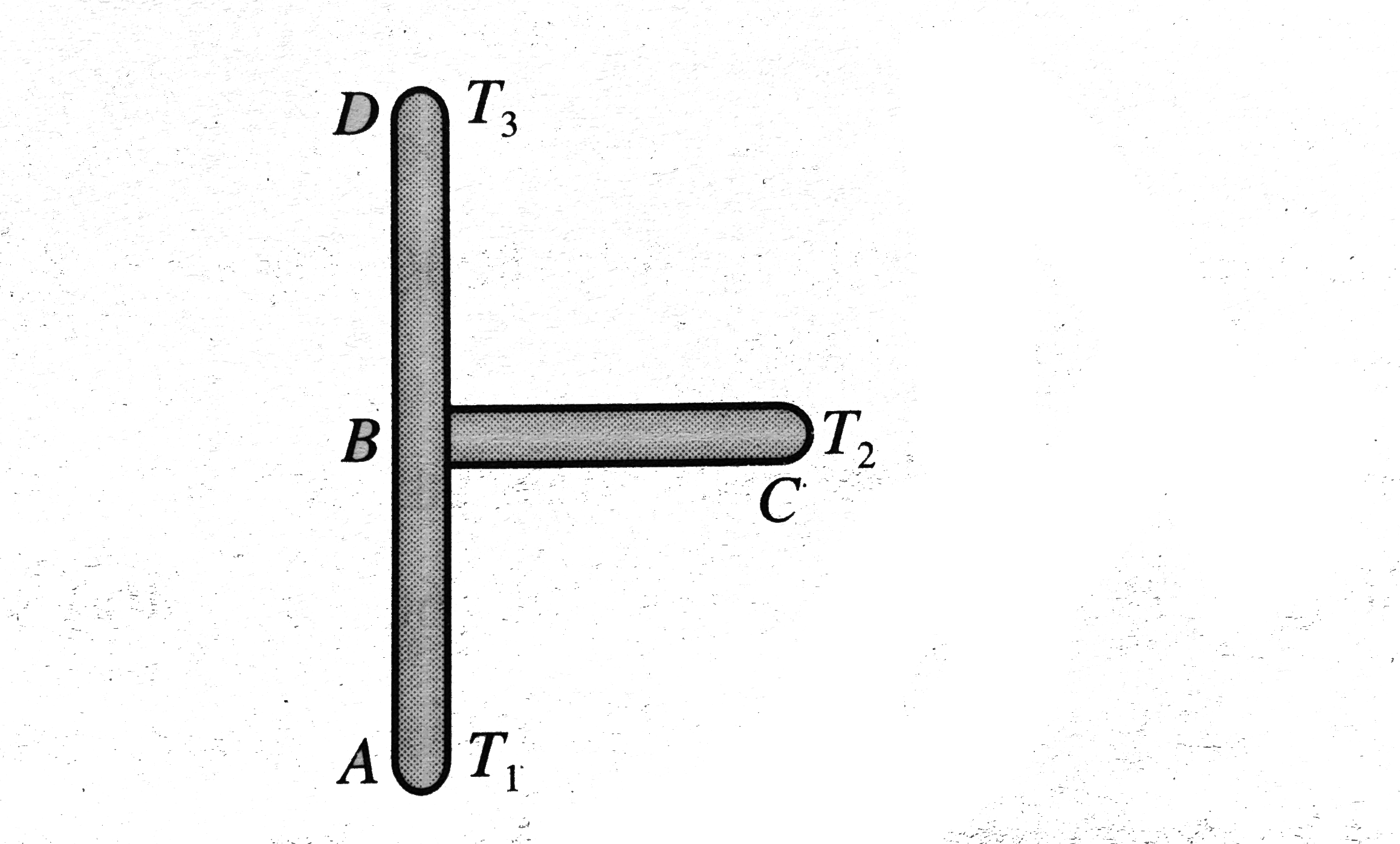
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionThree perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionThree perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
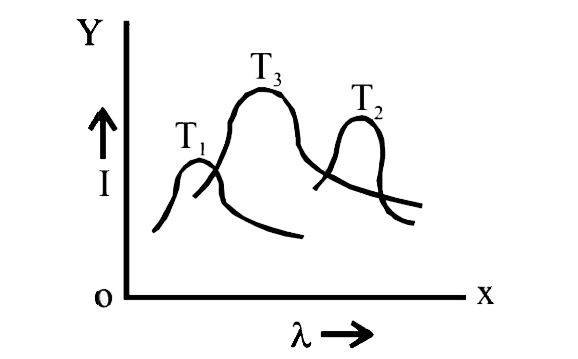
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
View Solution
