Three perfect gases at absolute temperature T1,T2,andT3 are mixed. The masses of molecules are n1,n2andn3 respectively. Assuming to loss of energy, the final temperature of the mixture is:
T1+T2+T33
n21T1+n22T2+n23T3n1+n2+n3
n1T1+n2T2+n3T3n1+n2+n3
T1+T2+T3n1+n2+n3
The correct Answer is:C
To find the final temperature of a mixture of three perfect gases at absolute temperatures T1,T2, and T3 with respective masses of molecules n1,n2, and n3, we can follow these steps:
Step 1: Understand the Kinetic Energy of Gases
The average kinetic energy E of a single molecule of a gas is given by the formula:
E=f2kT
where f is the degrees of freedom, k is the Boltzmann constant, and T is the absolute temperature.
Step 2: Total Kinetic Energy of Each Gas
For n1 molecules of the first gas at temperature T1, the total kinetic energy E1 is:
E1=n1⋅f2kT1
Similarly, for the second gas with n2 molecules at temperature T2:
E2=n2⋅f2kT2
And for the third gas with n3 molecules at temperature T3:
E3=n3⋅f2kT3
Step 3: Total Initial Energy of the Mixture
The total initial energy Einitial of the mixture is the sum of the energies of the three gases:
Einitial=E1+E2+E3=n1⋅f2kT1+n2⋅f2kT2+n3⋅f2kT3
Step 4: Total Number of Molecules
The total number of molecules in the mixture is:
N=n1+n2+n3
Step 5: Final Energy of the Mixture
Assuming no loss of energy, the final energy Efinal of the mixture can be expressed as:
Efinal=N⋅f2kTe
where Te is the final temperature of the mixture.
Step 6: Equating Initial and Final Energy
By the conservation of energy, we set the total initial energy equal to the total final energy:
n1⋅f2kT1+n2⋅f2kT2+n3⋅f2kT3=(n1+n2+n3)⋅f2kTe
Step 7: Simplifying the Equation
We can cancel f2k from both sides:
n1T1+n2T2+n3T3=(n1+n2+n3)Te
Step 8: Solving for Final Temperature
Now, we can solve for Te:
Te=n1T1+n2T2+n3T3n1+n2+n3
Final Answer
Thus, the final temperature of the mixture is:
Te=n1T1+n2T2+n3T3n1+n2+n3
The average kinetic energy E of a single molecule of a gas is given by the formula:
E=f2kT
where f is the degrees of freedom, k is the Boltzmann constant, and T is the absolute temperature.
For n1 molecules of the first gas at temperature T1, the total kinetic energy E1 is:
E1=n1⋅f2kT1
Similarly, for the second gas with n2 molecules at temperature T2:
E2=n2⋅f2kT2
And for the third gas with n3 molecules at temperature T3:
E3=n3⋅f2kT3
The total initial energy Einitial of the mixture is the sum of the energies of the three gases:
Einitial=E1+E2+E3=n1⋅f2kT1+n2⋅f2kT2+n3⋅f2kT3
The total number of molecules in the mixture is:
N=n1+n2+n3
Assuming no loss of energy, the final energy Efinal of the mixture can be expressed as:
Efinal=N⋅f2kTe
where Te is the final temperature of the mixture.
By the conservation of energy, we set the total initial energy equal to the total final energy:
n1⋅f2kT1+n2⋅f2kT2+n3⋅f2kT3=(n1+n2+n3)⋅f2kTe
We can cancel f2k from both sides:
n1T1+n2T2+n3T3=(n1+n2+n3)Te
Now, we can solve for Te:
Te=n1T1+n2T2+n3T3n1+n2+n3
Thus, the final temperature of the mixture is:
Te=n1T1+n2T2+n3T3n1+n2+n3
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - C Previous Years Questions
21 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - A Objective Type Questions
30 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
Three perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionThree perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionTwo perfect gases at absolute temperature T1andT2 are mixed. There is no loss of energy. The masses of the molecules are m1andm2. The number of molecules in the gases are n1andn2. The temperature of the mixture is
View SolutionTwo perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View SolutionTwo perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View SolutionFour thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
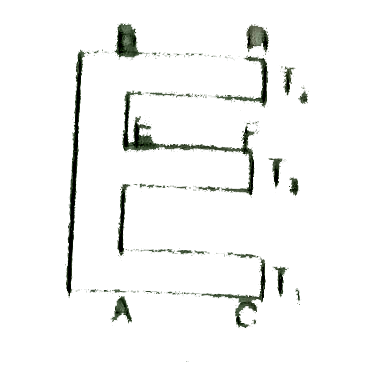
View SolutionThree liquids with masses m1,m2,m3 are throughly mixed. If their specific heats are c1,c2,c3 and their temperature T1,T2,T3, respectively, then the temperature of the mixture is
View SolutionA container has N molecules at absolute temperature T. If the number of molecules is doubled but kinetic energy in box remains the same as before, the absolute temperature of the gas is
View SolutionA container has N molecules at absolute temperature T. If the number of molecules is doubled but kinetic energy in box remains the same as before, the absolute temperature of the gas is
View SolutionTwo gases A and B having the same pressure P, volume V and temperature T are mixed. If mixture has volume and temperature as V and T respectively, then the pressure of the mixture will be
View Solution
