Three particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
To find the time of meeting of the three particles A, B, and C, we can follow these steps:
Step 1: Understand the setup
We have three particles A, B, and C located at the vertices of an equilateral triangle with side length r. Each particle moves towards the next particle: A moves towards B, B moves towards C, and C moves towards A, all with a constant speed v.
Step 2: Analyze the motion
As each particle moves towards the next, they will spiral inward towards a common point. We need to determine how long it will take for them to meet at that point.
Step 3: Define the meeting point
Let’s denote the meeting point as point O. We can draw a perpendicular from point O to the side BC of the triangle, meeting at point D. Since the triangle is equilateral, we can say that the distances from O to the midpoints of the sides will be equal.
Step 4: Calculate the distances
Let’s denote the distance from O to B (or O to A or O to C) as x. The angle between the line OB and the line BC is 60∘ because of the properties of the equilateral triangle.
Step 5: Use trigonometry to find relationships
From triangle OBD, we can use trigonometry:
- The vertical distance BD (which is half of side r) is r2.
- The angle OBD is 30∘.
Using the sine function:
sin(60∘)=BDOB=r2x
This gives us:
√32=r2x
From this, we can solve for x:
x=r√3
Step 6: Calculate the time of meeting
Now we can find the time T it takes for the particles to meet. The velocity component of each particle towards the center is given by:
veffective=vcos(30∘)=v⋅√32
Thus, the time T can be expressed as:
T=distancevelocity=xv⋅√32=r√3v⋅√32
Simplifying this gives:
T=2r3v
Final Answer
The time of their meeting is:
T=2r3v
We have three particles A, B, and C located at the vertices of an equilateral triangle with side length r. Each particle moves towards the next particle: A moves towards B, B moves towards C, and C moves towards A, all with a constant speed v.
As each particle moves towards the next, they will spiral inward towards a common point. We need to determine how long it will take for them to meet at that point.
Let’s denote the meeting point as point O. We can draw a perpendicular from point O to the side BC of the triangle, meeting at point D. Since the triangle is equilateral, we can say that the distances from O to the midpoints of the sides will be equal.
Let’s denote the distance from O to B (or O to A or O to C) as x. The angle between the line OB and the line BC is 60∘ because of the properties of the equilateral triangle.
From triangle OBD, we can use trigonometry:
- The vertical distance BD (which is half of side r) is r2.
- The angle OBD is 30∘.
sin(60∘)=BDOB=r2x
This gives us:
√32=r2x
From this, we can solve for x:
x=r√3
Now we can find the time T it takes for the particles to meet. The velocity component of each particle towards the center is given by:
veffective=vcos(30∘)=v⋅√32
Thus, the time T can be expressed as:
T=distancevelocity=xv⋅√32=r√3v⋅√32
Simplifying this gives:
T=2r3v
The time of their meeting is:
T=2r3v
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Three insects A,B and C are situated at the vertices of an equillateral triangle of side 1. the insect A heads towards B,B towards C,C towards A with constant speeds v such that they always remain at the vertices of an equilateral triangle. Find the (a) time of their meeting (b) equation of path traced by one insect relative to the other.
View SolutionThree boys A,B and C are situated at the vertices of an equilateral triangle of side d at t=0. Each of the boys moves with constant speed v. A always moves towards C and C towards A, At what time and where they meet each other?
View Solution
Knowledge Check
Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2LThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
At=dvBt=3d2vCt=2d3vDt=0Three particles A,B and C situated at vertices of an equilateral triangle, all moving with same constant speed such that A always move towards B,B always towards C and C always towards A. Initial seperation between each of the particle is a. O is the centroid of the triangle. Distance covered by particle A when it completes one revolution around O is
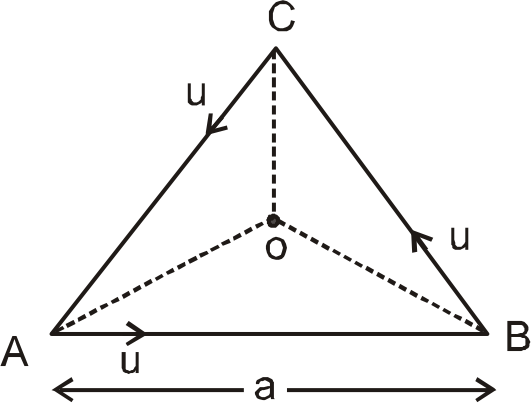A2a(1−e−2√3π)B2a3(1−e−2√3π)Ca(1+e−2√3π)D2a3(1−e−√3π)
Show that the points (a,b,c),(b,c,a),(c,a,b) are the vertices of an equilateral triangle.
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
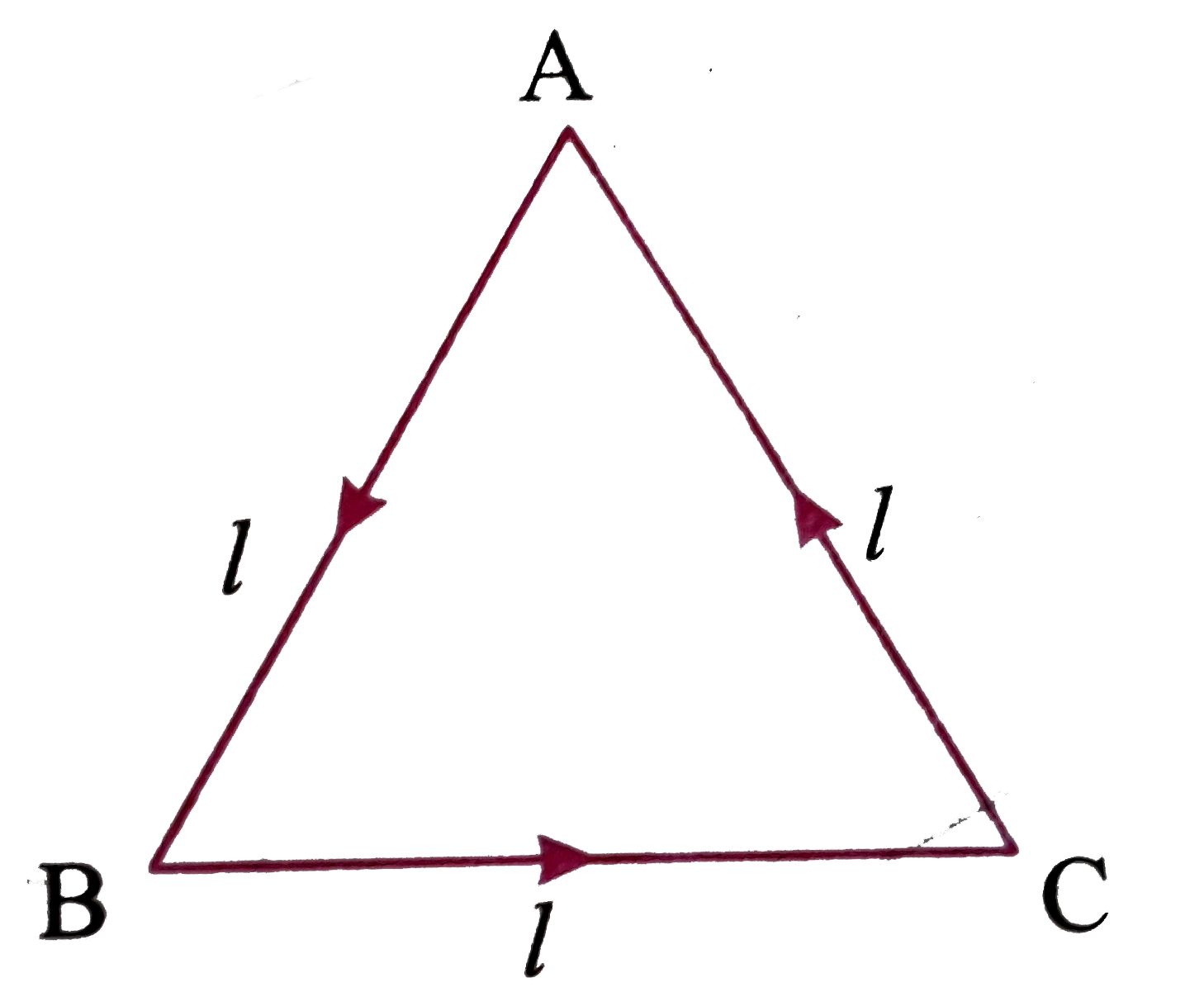
View SolutionThree particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
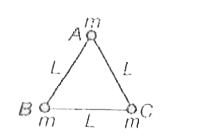
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
View Solution