Three particles x, y, z are placed in a line as shown in the figure. A fourth particle at O is also placed at a perpendicular bisector of line xz. Calculate the total gravitational force at O. All the particle are of some mass.

Fx = Force at O due to x=Gm22s2 along Ox
Fy = Force at O due to y=Gm22s2 along Oy
Fz = Force at O due to z=Gm22s2 along Oz
The resultant of all forces Fx,Fy,Fz will be along Oy.
Component of Fx along Oy=Fxcos45∘
=Gm22√2s2
Component of Fy along Oy
=Gm2s2
Component of Fy along Oy=Fycos45∘=Gm22√2s2
Hence, the resultant of all of the forces is
F=Gm2s22√2+Gm2s2+Gm22√2s2
=Gm2s2(12√2+12√2+1) along Oy

Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (TEXTBOOK EXERCISES)
23 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (Additional Exercises)
4 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Conceptual Questions
19 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
A particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
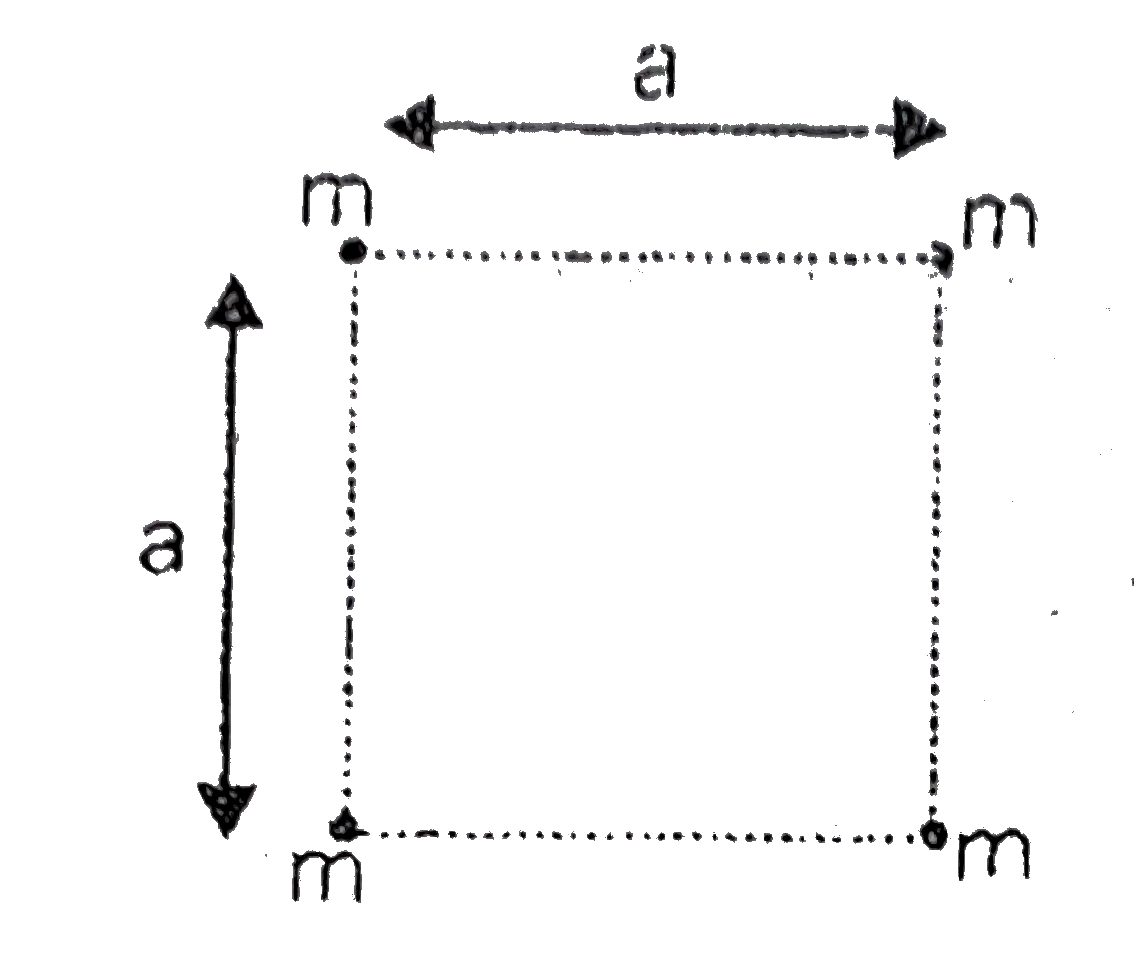
View SolutionFour point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
 .
.
View Solution
Knowledge Check
A particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
 AIncreasesBDecreasesCRemains constantDFirst increases and then decreases
AIncreasesBDecreasesCRemains constantDFirst increases and then decreasesMass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
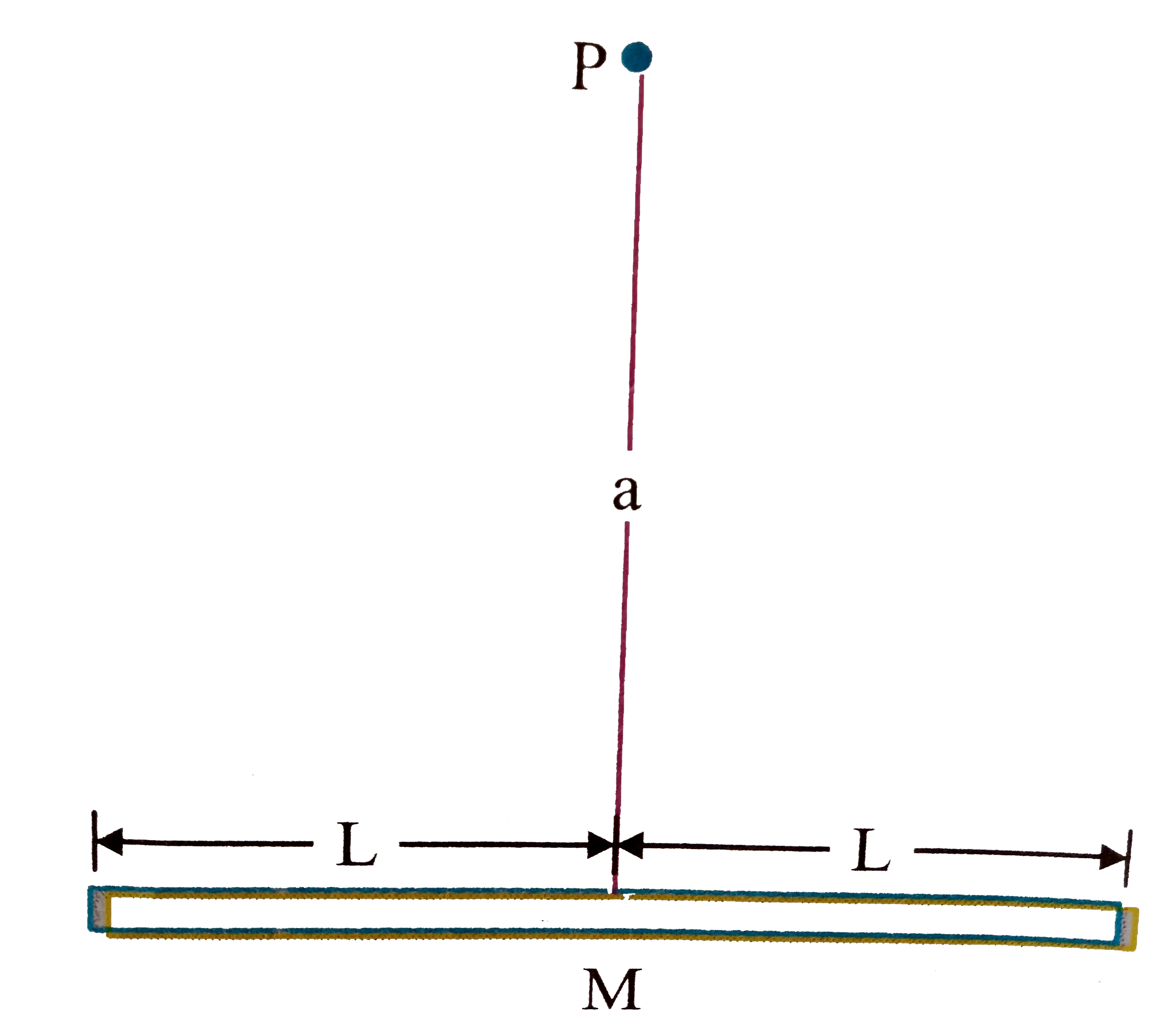 AGMm√L2+a2BGMma(L2+a2)CGMma√L2+a2DGMma(L2+a2)2
AGMm√L2+a2BGMma(L2+a2)CGMma√L2+a2DGMma(L2+a2)2Two particles are placed at some distance. If the mass of each of the two particles is doubled, keeping the distance between them unchanged, the value of gravitational force between them will be
A14timesB4 timesC12timesDunchanged
Four point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
 .
.
View SolutionTwo particles are placed at some distance. If the mass of each of the two particles is doubled, keeping the distance between them unchanged, the value of gravitational force between them will be
View SolutionThree portion A , B and C each of mass re placed ina line with AB=BC=d. Find the gravittional force on a fourth article P of same mass placed at a distance d from the particle B on the perpendicular bisector of the line AC.
View SolutionTwo particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo particles each of mass 'm' are placed at A and C are such AB=BC=L. The gravitational force on the third particle placed at D at a distance L on the perpendicular bisector of the line AC is
View Solution
