Three planets of same density have radii R1,R2 and R3 such that R1=2R2=3R3. The gravitational field at their respective surfaces are g1,g2 and g3 and escape velocities from their surfeces are υ1,υ2 and υ3, then
g1/g2=2
g1/g3=3
υ1/υ2=1/4
υ1/υ3=3
The correct Answer is:A, B, D
To solve the problem, we need to derive the relationships between the gravitational fields and escape velocities of the three planets based on their radii.
1. Understanding the Relationship Between Radii:
Given that R1=2R2=3R3, we can express the radii in terms of R3:
R1=6R3,R2=3R3,R3=R3
2. Gravitational Field at the Surface of a Planet:
The gravitational field g at the surface of a planet is given by:
g=GMR2
where M is the mass of the planet and R is its radius.
3. Mass of the Planet:
The mass M can be expressed in terms of density ρ and volume V:
M=ρV=ρ(43πR3)
Substituting this into the equation for g:
g=G(ρ43πR3)R2=4πGρ3R
This shows that g is directly proportional to R.
4. Calculating Gravitational Fields:
Using the relationship derived, we can express the gravitational fields for the three planets:
g1=4πGρ3R1,g2=4πGρ3R2,g3=4πGρ3R3
Now substituting the values of R1, R2, and R3:
g1=4πGρ3(6R3)=8g3,g2=4πGρ3(3R3)=4g3
5. Finding Ratios of Gravitational Fields:
Now we can find the ratios:
g1g2=8g34g3=2andg1g3=8g3g3=8
6. Escape Velocity Formula:
The escape velocity v from the surface of a planet is given by:
v=√2gR
Substituting for each planet:
v1=√2g1R1,v2=√2g2R2,v3=√2g3R3
7. Calculating Escape Velocities:
Using the gravitational fields we derived:
v1=√2⋅8g3⋅6R3=√96g3R3,v2=√2⋅4g3⋅3R3=√24g3R3,v3=√2g3R3
8. Finding Ratios of Escape Velocities:
Now we can find the ratios:
v1v2=√96g3R3√24g3R3=√4=2
v1v3=√96g3R3√2g3R3=√48=4√3
Summary of Results:
- g1g2=2
- g1g3=8
- v1v2=2
- v1v3=4√3
Given that R1=2R2=3R3, we can express the radii in terms of R3:
R1=6R3,R2=3R3,R3=R3
The gravitational field g at the surface of a planet is given by:
g=GMR2
where M is the mass of the planet and R is its radius.
The mass M can be expressed in terms of density ρ and volume V:
M=ρV=ρ(43πR3)
Substituting this into the equation for g:
g=G(ρ43πR3)R2=4πGρ3R
This shows that g is directly proportional to R.
Using the relationship derived, we can express the gravitational fields for the three planets:
g1=4πGρ3R1,g2=4πGρ3R2,g3=4πGρ3R3
Now substituting the values of R1, R2, and R3:
g1=4πGρ3(6R3)=8g3,g2=4πGρ3(3R3)=4g3
Now we can find the ratios:
g1g2=8g34g3=2andg1g3=8g3g3=8
The escape velocity v from the surface of a planet is given by:
v=√2gR
Substituting for each planet:
v1=√2g1R1,v2=√2g2R2,v3=√2g3R3
Using the gravitational fields we derived:
v1=√2⋅8g3⋅6R3=√96g3R3,v2=√2⋅4g3⋅3R3=√24g3R3,v3=√2g3R3
Now we can find the ratios:
v1v2=√96g3R3√24g3R3=√4=2
v1v3=√96g3R3√2g3R3=√48=4√3
- g1g2=2
- g1g3=8
- v1v2=2
- v1v3=4√3
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionIn a ΔABC,r1+r2+r3−r=
View SolutionIn the situation shown, resistance R1,R2 and R3 are in the ratio 3:2:1 , then
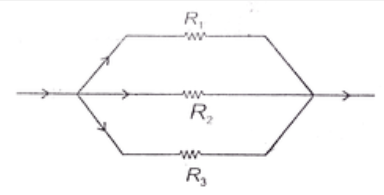
View SolutionTwo planets A and B have the same averge density . Their radii RAandRB are such that RA:RB=3:1. If gA and gB are the acceleration due to gravity at the surfaces of the planets, the gA:gB equals
View SolutionTwo planets A and B have the same average density . Their radii RAandRB are such that RA:RB=3:1 . If gAandgB are the acceleration due to gravity at the surface of the planets , the gA:gB equals
View SolutionTwo planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
View SolutionTwo planets of radii R1 and R2 have masses m1 and M2 such that M1M2=1g. The weight of an object on these planets is w1 and w2 such that w1w2=49. The ratio R1R2
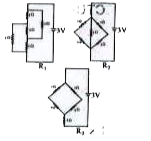
View SolutionFig shows three resistor configuration R1,R2andR3 connected to 3V battery. If the power dissipated by the configuration R1,R2andR3 is P1,P2andP3 respectively, then
View SolutionIf in a Δ the ex-reddii r1r2r3 are in the ratio 1:2:3 then their sides are in the ratio :-
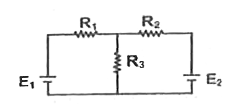
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
View Solution
