Two planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
3
1
2
4
The correct Answer is:D
To solve the problem, we need to find the ratio of escape velocities from the surfaces of two planets with given masses and radii. Let's denote the escape velocities from the surfaces of the two planets as v1 and v2.
1. Understand the formula for escape velocity:
The escape velocity v from the surface of a planet is given by the formula:
v=√2GMR
where G is the universal gravitational constant, M is the mass of the planet, and R is the radius of the planet.
2. Identify the masses and radii of the planets:
- For Planet 1: Mass M1=M and Radius R1=R
- For Planet 2: Mass M2=M2 and Radius R2=R2
3. Calculate the escape velocities for both planets:
- For Planet 1:
v1=√2GM1R1=√2GMR
- For Planet 2:
v2=√2GM2R2=
⎷2G⋅M2R2=√2G⋅M2⋅2R=√2GMR=v1
4. Find the ratio of escape velocities:
Now, we can find the ratio of the escape velocities:
v1v2=√2GMR√2GMR=1
5. Relate the ratio to the given condition:
According to the problem, we have:
v1v2=n4
Setting this equal to our calculated ratio:
1=n4
6. Solve for n:
To find n, we multiply both sides by 4:
n=4
Conclusion:
The value of n is 4.
The escape velocity v from the surface of a planet is given by the formula:
v=√2GMR
where G is the universal gravitational constant, M is the mass of the planet, and R is the radius of the planet.
- For Planet 1: Mass M1=M and Radius R1=R
- For Planet 2: Mass M2=M2 and Radius R2=R2
- For Planet 1:
v1=√2GM1R1=√2GMR
- For Planet 2:
v2=√2GM2R2=
⎷2G⋅M2R2=√2G⋅M2⋅2R=√2GMR=v1
Now, we can find the ratio of the escape velocities:
v1v2=√2GMR√2GMR=1
According to the problem, we have:
v1v2=n4
Setting this equal to our calculated ratio:
1=n4
To find n, we multiply both sides by 4:
n=4
The value of n is 4.
Topper's Solved these Questions
Similar Questions
The ratio of the masses and radii of two planets are 2:3 and 8:27.The ratio of respective escape speeds from their surfaces are
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionThe ratio of the masses and radii of two planets are 2 : 3 and 4 : 9. What is the ratio of the escape speed at their surface ?
View SolutionThe ratio of the masses and radii of two planets are 2 : 3 and 4 : 9. What is the ratio of the escape speed at their surface ?
View SolutionThe ratio of the masses and radii of two planets are 4:6and8:18. What is the ratio of the escape speed at their surface ?
View Solution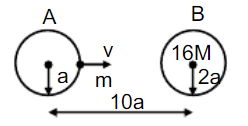
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their inertia.
View SolutionTwo racing cars of masses m and 4m are moving in circles of radii r and 2r respectively. If their speeds are such that each makes a complete circle in the same time, then the ratio of the angular speeds of the first to the second car is
View SolutionTwo balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare: Their momentum.
View SolutionPlanet A has massa M and radius R. Planet B has half the mass and half the radius of Planet A.If the escape velocities from the Planets A and B are vAandvB, respectively , then vAvB=n4. The vlaue of n is :
View Solution