Three point charges q, 2q and 8q are to be placed on a
. 9cm long straight line. Find the
. positions where the charges shouldbe placed such that the potential energy
. of this sysrem is minimum. In this situation, what is the
. electric field at the charge q due to the other two charges?
To solve the problem of placing the charges q, 2q, and 8q on a 9 cm long straight line such that the potential energy of the system is minimized, we can follow these steps:
Step 1: Understand the Arrangement of Charges
To minimize the potential energy, we should place the charges such that the larger charges are farther apart from each other. Thus, we can place charge q in between 2q and 8q.
Step 2: Assign Positions
Let’s denote the position of charge q as x cm from one end of the line. Therefore, the positions of the other charges will be:
- Charge 2q at position 0 cm.
- Charge 8q at position 9 cm.
- Charge q at position x cm.
Step 3: Calculate the Potential Energy
The potential energy U of the system can be expressed as the sum of the potential energies between each pair of charges:
U=k(q⋅2qx+q⋅8q9−x+2q⋅8q9)
Where k is Coulomb's constant.
Step 4: Simplify the Expression
Substituting the values:
U=kq2(2x+89−x+169)
Step 5: Differentiate to Find Minimum Potential Energy
To find the value of x that minimizes U, we need to differentiate U with respect to x and set the derivative equal to zero:
dUdx=−2kq2x2+8kq2(9−x)2=0
Step 6: Solve for x
Setting the derivative to zero gives:
2x2=8(9−x)2
Cross-multiplying and simplifying:
2(9−x)2=8x2
Expanding and rearranging:
2(81−18x+x2)=8x2⟹162−36x+2x2=8x2
6x2−36x+162=0⟹x2−6x+27=0
Using the quadratic formula:
x=6±√(−6)2−4⋅1⋅272⋅1
This results in:
x=3 cm
Step 7: Calculate Electric Field at Charge q
Now, we need to find the electric field at the position of charge q due to the other two charges 2q and 8q.
1. Electric Field due to 2q:
E2q=k⋅2q(3)2=2kq9 (towards right)
2. Electric Field due to 8q:
E8q=k⋅8q(6)2=8kq36=2kq9 (towards left)
Step 8: Calculate Net Electric Field
The net electric field at charge q is:
Enet=E2q−E8q=2kq9−2kq9=0
Final Answer
- The positions of the charges should be:
- q at 3 cm,
- 2q at 0 cm,
- 8q at 9 cm.
- The electric field at charge q due to the other two charges is 0.
To minimize the potential energy, we should place the charges such that the larger charges are farther apart from each other. Thus, we can place charge q in between 2q and 8q.
Let’s denote the position of charge q as x cm from one end of the line. Therefore, the positions of the other charges will be:
- Charge 2q at position 0 cm.
- Charge 8q at position 9 cm.
- Charge q at position x cm.
The potential energy U of the system can be expressed as the sum of the potential energies between each pair of charges:
U=k(q⋅2qx+q⋅8q9−x+2q⋅8q9)
Where k is Coulomb's constant.
Substituting the values:
U=kq2(2x+89−x+169)
To find the value of x that minimizes U, we need to differentiate U with respect to x and set the derivative equal to zero:
dUdx=−2kq2x2+8kq2(9−x)2=0
Setting the derivative to zero gives:
2x2=8(9−x)2
Cross-multiplying and simplifying:
2(9−x)2=8x2
Expanding and rearranging:
2(81−18x+x2)=8x2⟹162−36x+2x2=8x2
6x2−36x+162=0⟹x2−6x+27=0
Using the quadratic formula:
x=6±√(−6)2−4⋅1⋅272⋅1
This results in:
x=3 cm
Now, we need to find the electric field at the position of charge q due to the other two charges 2q and 8q.
E2q=k⋅2q(3)2=2kq9 (towards right)
E8q=k⋅8q(6)2=8kq36=2kq9 (towards left)
The net electric field at charge q is:
Enet=E2q−E8q=2kq9−2kq9=0
- The positions of the charges should be:
- q at 3 cm,
- 2q at 0 cm,
- 8q at 9 cm.
- The electric field at charge q due to the other two charges is 0.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionThree point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
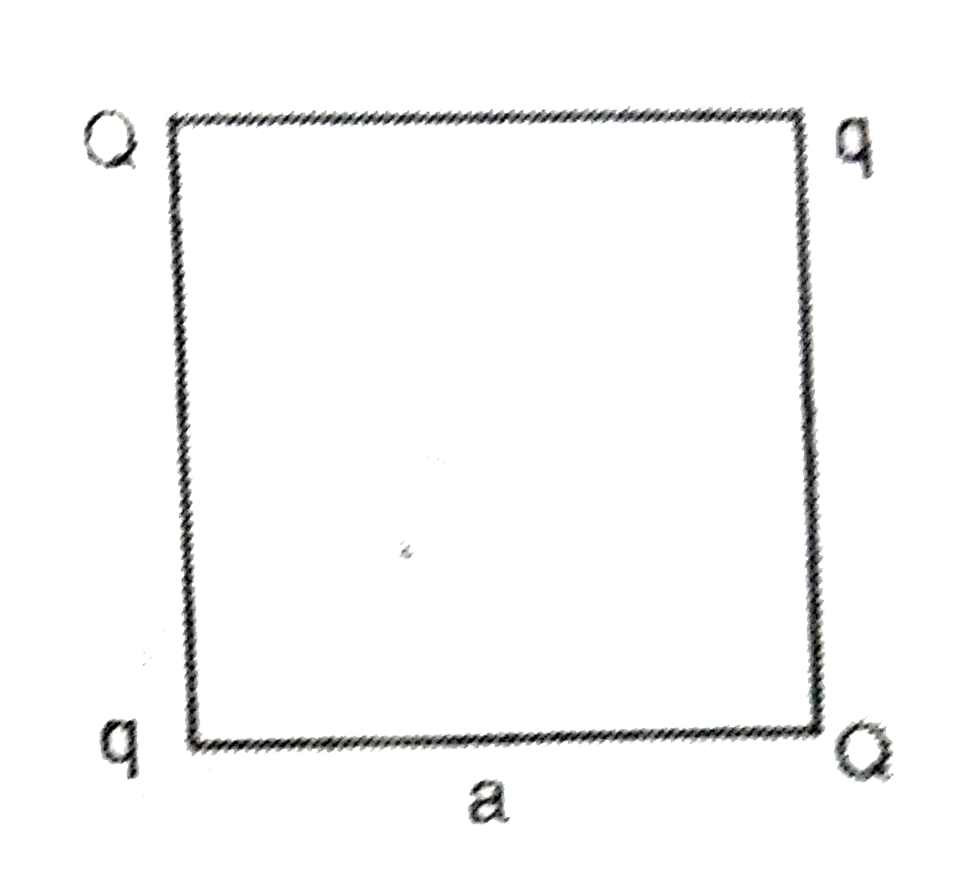
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
View SolutionTwo electric charges q1=qandq2=−2q are placed at a distance l = 6a apart. Find the locus of points in the plane of the charges where the field potential is zero
View SolutionTwo point charges +4q and +q are placed 30cm apart. At what point on the line joining them is the electric field zero
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionA charge q is placed st the centre of a spher. Taking outward normal as positive, find the flux of the electric field through the surface of the sphere due to the enclosed charge.
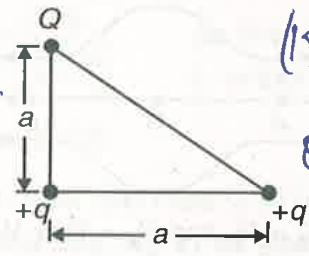
View SolutionThree charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
View SolutionTwo equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionThree charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View Solution
