Three point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
4Q and 16Q must be at the ends and Q at a distance of 3 cm from the 16Q
4Q and 16Q must be at the ends and Q at a distance of 6 cm from the 16Q
Electric field at the position of Q is zero
Electric field at the position of Q is Q4πε0
The correct Answer is:B, C
To solve the problem of arranging the point charges Q,4Q, and 16Q on a straight line of length 9 cm for minimum potential energy, we can follow these steps:
Step 1: Understanding the Arrangement
We need to place the charges Q,4Q, and 16Q on a straight line such that the potential energy of the system is minimized. The potential energy U between two point charges is given by:
U=kQ1Q2r
where k is Coulomb's constant, Q1 and Q2 are the magnitudes of the charges, and r is the distance between them.
Step 2: Placing the Largest Charges at the Ends
To minimize the potential energy, we should place the two larger charges, 4Q and 16Q, at the ends of the line. This is because potential energy is inversely proportional to the distance between charges, and placing larger charges further apart will reduce their contribution to the overall potential energy.
Step 3: Positioning the Charge Q
Let’s denote the positions of the charges as follows:
- Place 4Q at position x=0 cm.
- Place 16Q at position x=9 cm.
- Let the charge Q be placed at position x cm, where 0<x<9.
Step 4: Finding the Distance
The distances from Q to the other charges are:
- Distance from 4Q to Q: x
- Distance from 16Q to Q: 9−x
Step 5: Writing the Total Potential Energy
The total potential energy U of the system can be expressed as:
U=k(4Q⋅Qx+16Q⋅Q9−x+4Q⋅16Q9)
The last term is constant and does not depend on x.
Step 6: Minimizing the Potential Energy
To find the value of x that minimizes U, we take the derivative of U with respect to x and set it to zero:
dUdx=−k(4Q2x2−16Q2(9−x)2)=0
This leads to:
4x2=16(9−x)2
Step 7: Solving the Equation
Cross-multiplying gives:
4(9−x)2=16x2
Expanding and simplifying:
4(81−18x+x2)=16x2
324−72x+4x2=16x2
0=12x2+72x−324
Dividing through by 12:
x2+6x−27=0
Using the quadratic formula x=−b±√b2−4ac2a:
x=−6±√36+1082=−6±122
This gives us:
x=3(valid)orx=−9(not valid)
Step 8: Conclusion
Thus, the charge Q should be placed 3 cm from 4Q and 6 cm from 16Q. Therefore, the correct arrangement is:
- 4Q at 0 cm
- Q at 3 cm
- 16Q at 9 cm
We need to place the charges Q,4Q, and 16Q on a straight line such that the potential energy of the system is minimized. The potential energy U between two point charges is given by:
U=kQ1Q2r
where k is Coulomb's constant, Q1 and Q2 are the magnitudes of the charges, and r is the distance between them.
To minimize the potential energy, we should place the two larger charges, 4Q and 16Q, at the ends of the line. This is because potential energy is inversely proportional to the distance between charges, and placing larger charges further apart will reduce their contribution to the overall potential energy.
Let’s denote the positions of the charges as follows:
- Place 4Q at position x=0 cm.
- Place 16Q at position x=9 cm.
- Let the charge Q be placed at position x cm, where 0<x<9.
The distances from Q to the other charges are:
- Distance from 4Q to Q: x
- Distance from 16Q to Q: 9−x
The total potential energy U of the system can be expressed as:
U=k(4Q⋅Qx+16Q⋅Q9−x+4Q⋅16Q9)
The last term is constant and does not depend on x.
To find the value of x that minimizes U, we take the derivative of U with respect to x and set it to zero:
dUdx=−k(4Q2x2−16Q2(9−x)2)=0
This leads to:
4x2=16(9−x)2
Cross-multiplying gives:
4(9−x)2=16x2
Expanding and simplifying:
4(81−18x+x2)=16x2
324−72x+4x2=16x2
0=12x2+72x−324
Dividing through by 12:
x2+6x−27=0
Using the quadratic formula x=−b±√b2−4ac2a:
x=−6±√36+1082=−6±122
This gives us:
x=3(valid)orx=−9(not valid)
Thus, the charge Q should be placed 3 cm from 4Q and 6 cm from 16Q. Therefore, the correct arrangement is:
- 4Q at 0 cm
- Q at 3 cm
- 16Q at 9 cm
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
Three point charges q, 2q and 8q are to be placed on a
. 9cm long straight line. Find the
. positions where the charges shouldbe placed such that the potential energy
. of this sysrem is minimum. In this situation, what is the
. electric field at the charge q due to the other two charges?
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.

View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo free point charges +qand+4q are placed apart a distance x. A third charge is so placed that all the three charges are in equilibrium. Then
View SolutionThree charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ is
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View SolutionFour point charges each +q is placed on the circumference of a circle of diameter 2d in such a way that they form a square. The potential at the centre is
View SolutionThree charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
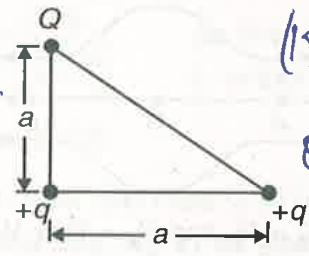
View SolutionThreee charges +Q1,+Q2 and q are placed on a straight line such that q is somewhere in between +Q1and Q2. If this system of charges is in equlibirium what should be the magnitude and sign of charge q?
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View Solution
