Three poistive charges of equal value q are placed at the vertices of an equilateral triangle. The resulting lines of force should be sketched as in




To solve the problem of sketching the electric field lines due to three positive charges placed at the vertices of an equilateral triangle, we can follow these steps:
1. Understanding the Configuration:
- We have three positive charges, each of value q, placed at the vertices of an equilateral triangle. Let’s denote the vertices as A, B, and C.
2. Identifying the Electric Field:
- Electric field lines originate from positive charges and point away from them. Therefore, the electric field lines will emanate outward from each of the three charges.
3. Symmetry Consideration:
- Due to the symmetry of the configuration, the electric field at the centroid (the center point of the triangle) will be zero. This is because the contributions to the electric field from each charge will cancel each other out at that point.
4. Electric Field at Midpoints:
- At the midpoints of each side of the triangle, the electric field will not be zero. The direction of the electric field lines at these points will be directed away from the charges at the vertices.
5. Sketching the Electric Field Lines:
- Start sketching the electric field lines emanating from each charge. The lines should:
- Move outward from each charge.
- Not intersect with each other.
- Not form closed loops, as electric field lines in electrostatics do not form closed loops.
6. Analyzing Options:
- Now, we need to analyze the provided options (A, B, C, D) based on the characteristics of the electric field lines we have just described:
- Option A: Forms a closed loop and incorrect direction - Incorrect.
- Option B: Also forms a closed loop and incorrect direction - Incorrect.
- Option C: No closed loops and correct direction - Correct.
- Option D: Forms a closed loop and lacks direction - Incorrect.
7. Conclusion:
- Based on the analysis, the correct option that represents the electric field lines due to the three positive charges is Option C.
- We have three positive charges, each of value q, placed at the vertices of an equilateral triangle. Let’s denote the vertices as A, B, and C.
- Electric field lines originate from positive charges and point away from them. Therefore, the electric field lines will emanate outward from each of the three charges.
- Due to the symmetry of the configuration, the electric field at the centroid (the center point of the triangle) will be zero. This is because the contributions to the electric field from each charge will cancel each other out at that point.
- At the midpoints of each side of the triangle, the electric field will not be zero. The direction of the electric field lines at these points will be directed away from the charges at the vertices.
- Start sketching the electric field lines emanating from each charge. The lines should:
- Move outward from each charge.
- Not intersect with each other.
- Not form closed loops, as electric field lines in electrostatics do not form closed loops.
- Now, we need to analyze the provided options (A, B, C, D) based on the characteristics of the electric field lines we have just described:
- Option A: Forms a closed loop and incorrect direction - Incorrect.
- Option B: Also forms a closed loop and incorrect direction - Incorrect.
- Option C: No closed loops and correct direction - Correct.
- Option D: Forms a closed loop and lacks direction - Incorrect.
- Based on the analysis, the correct option that represents the electric field lines due to the three positive charges is Option C.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
Three positive charges of equal magnitude q are placed at the vertics of and equilatral triangle of side l. How can the system of charges be palced in equilibrium?
View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View Solution
Knowledge Check
- Question 1 - Select One
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View SolutionThree point charges q are placed on vertices of an equilateral triangle of side length a. The charge Q that should be kept at centroid of triangle such that the system is in equilibrium is equal to
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
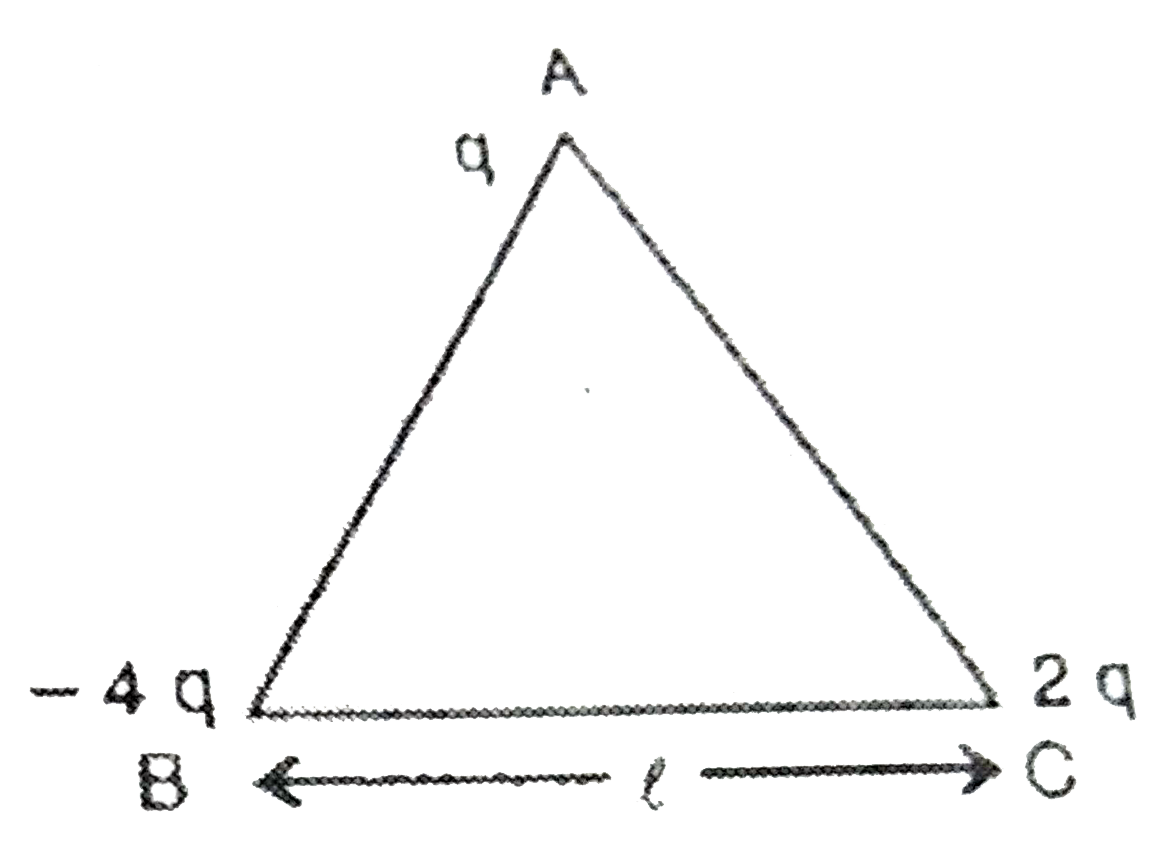
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.
 View Solution
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View Solution
