Three resistances of 4Ω each are connected as shown in figure. If the point D divides the resistance into two equal halves, the resistance between point A and D will be:
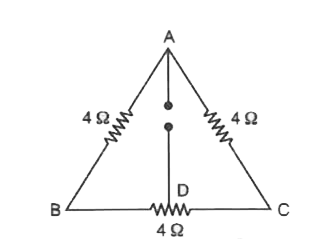
12Ω
6Ω
3Ω
1/3Ω
The correct Answer is:C
ABD, ACD are in series. They are connected in parallel
i.e., 16+16=13 i.e., R=3Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:MULTIPLE CHOICE QUESTIONS ( LEVEL-II)
Explore 54 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:MULTIPLE CHOICE QUESTIONS (PARAGRAPH QUESTIONS)
Explore 2 Videos
- ATOMS, MOLECULES AND NUCLEIBook:MODERN PUBLICATIONChapter:ATOMS, MOLECULES AND NUCLEIExercise:Recent Competitive Questions
Explore 40 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION Book:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN ONE DIMENSION Exercise:Revision Test
Explore 45 Videos
Similar Questions
Three resistances of 4Ω each are connected as shown in the figure. If point D divides the resistance into two equal halves , the resistance between points A and D will be
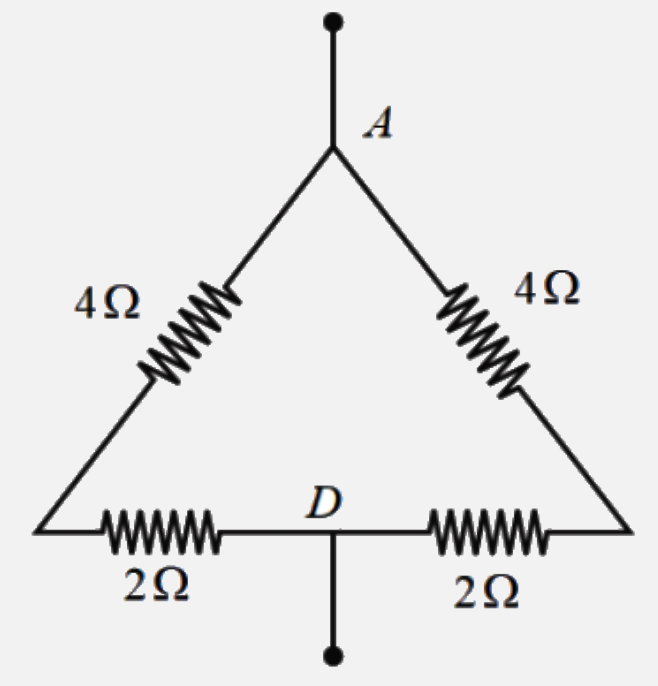
View SolutionThree resistances of 4Ω each are connected as shown in the figure. If point D divides the resistance into two equal halves , the resistance between points A and D will be

View Solution
Knowledge Check
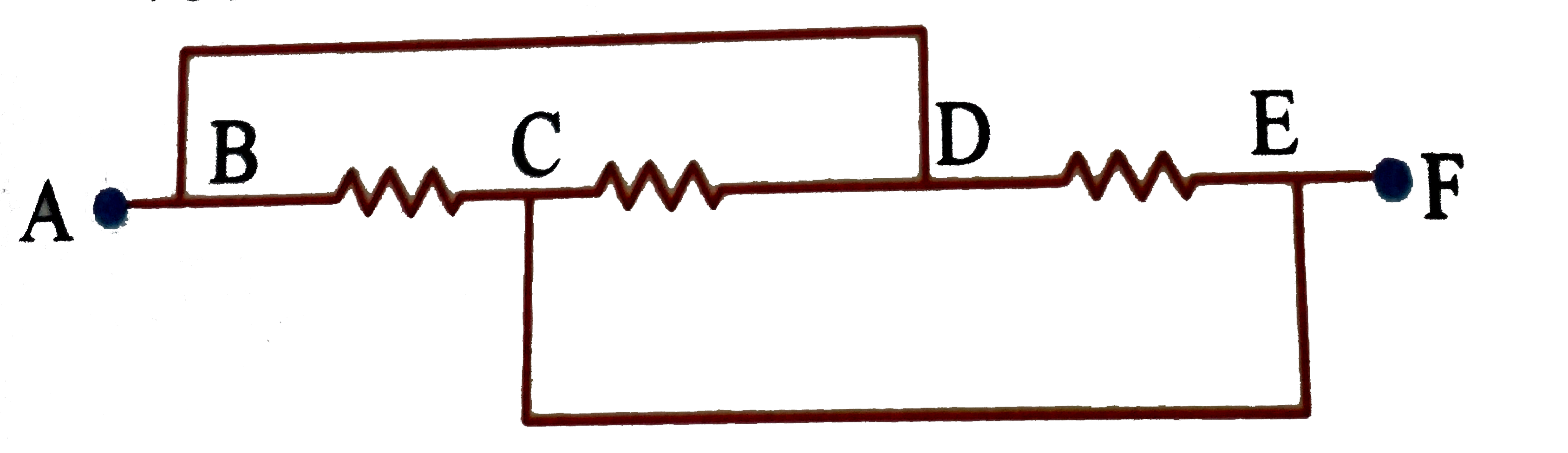
Three resistances each of 3Ω are connected as shown in fig. the resultant resistance between A and F isA9ΩB2ΩC4ΩD1ΩIn the same figure, equivalent resistance between points A and D is
AR4B2RCRDR2Five equal resistances of 10Ω are connected between A and B as shown in figure. The resultant resistance
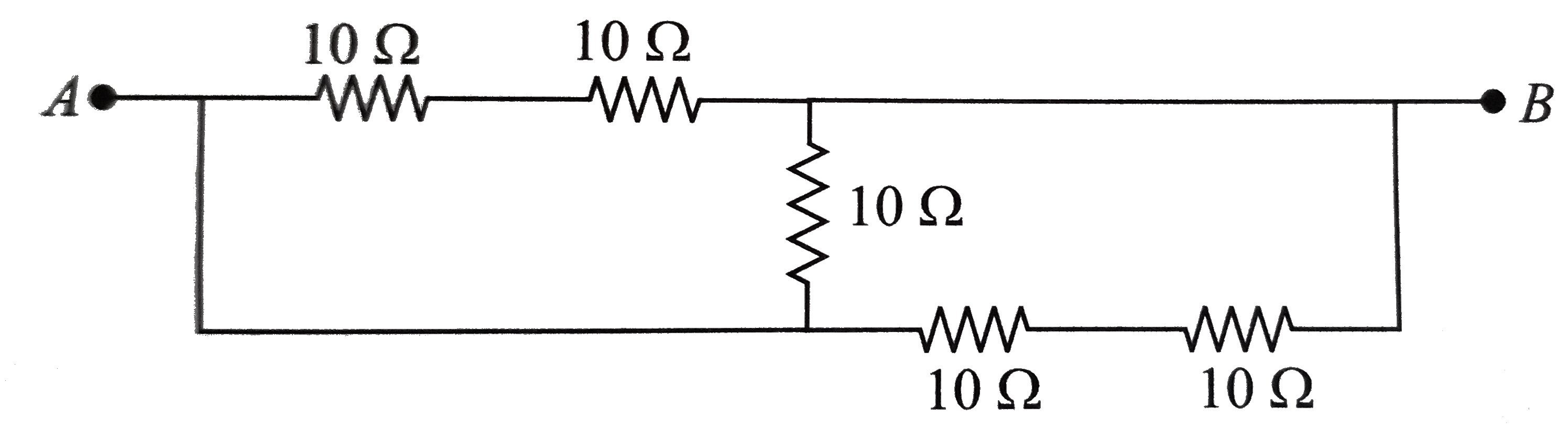 A10ΩB5ΩC15ΩD6Ω
A10ΩB5ΩC15ΩD6Ω
Three resistances 5Ω,5Ω and 6Ω are connected as shown in figure. If the point S divides the resistance 6Ω into two equal halves, the resistance between points P and S is
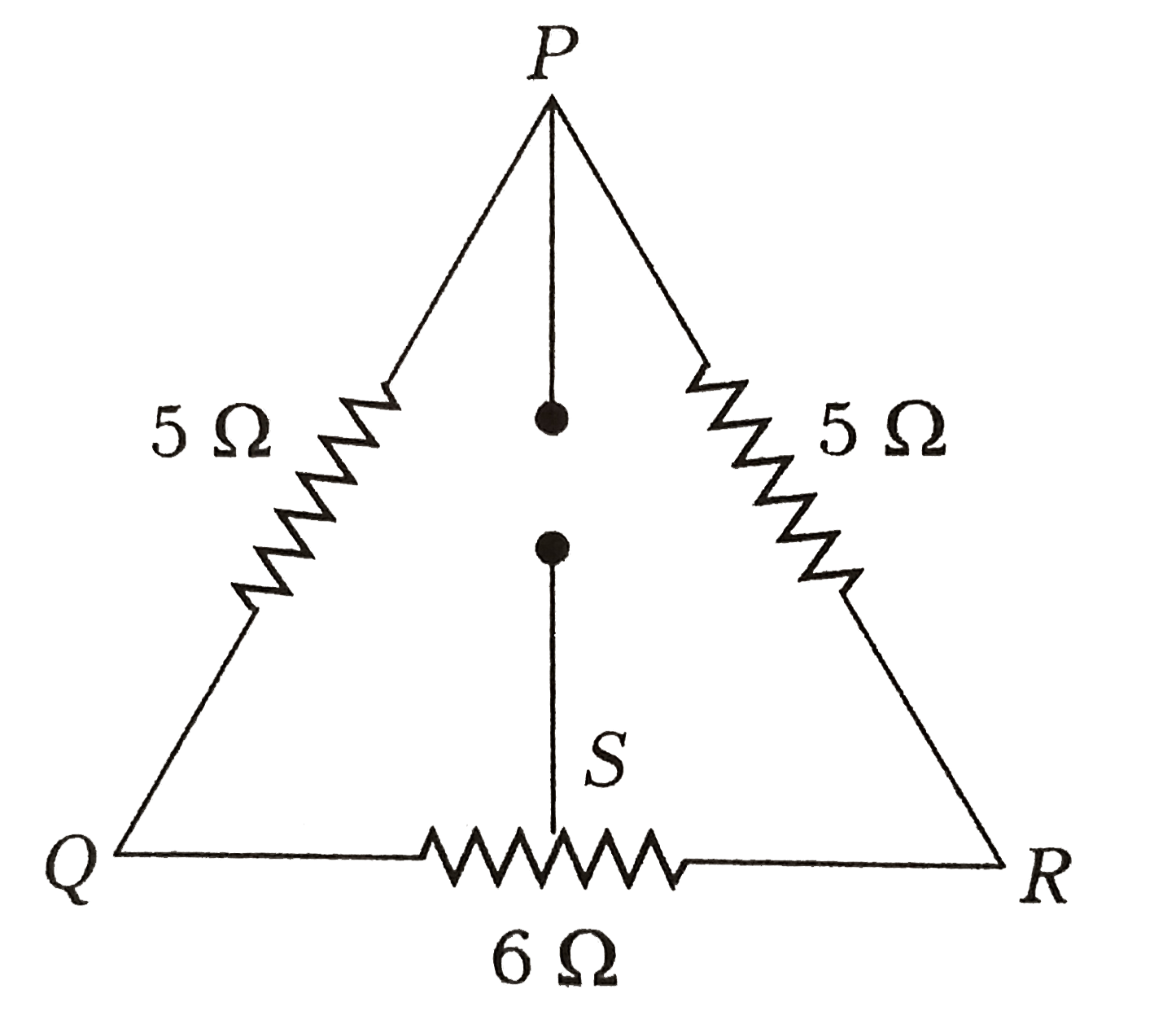
View SolutionThree resistances 5Ω,5Ω and 6Ω are connected as shown in figure. If the point S divides the resistance 6Ω into two equal halves, the resistance between points P and S is

View SolutionIn the same figure, equivalent resistance between points A and D is
View SolutionIn the network shown in the figure, each of the resistance is equal to 2Ω . The resistance between the point A and B is
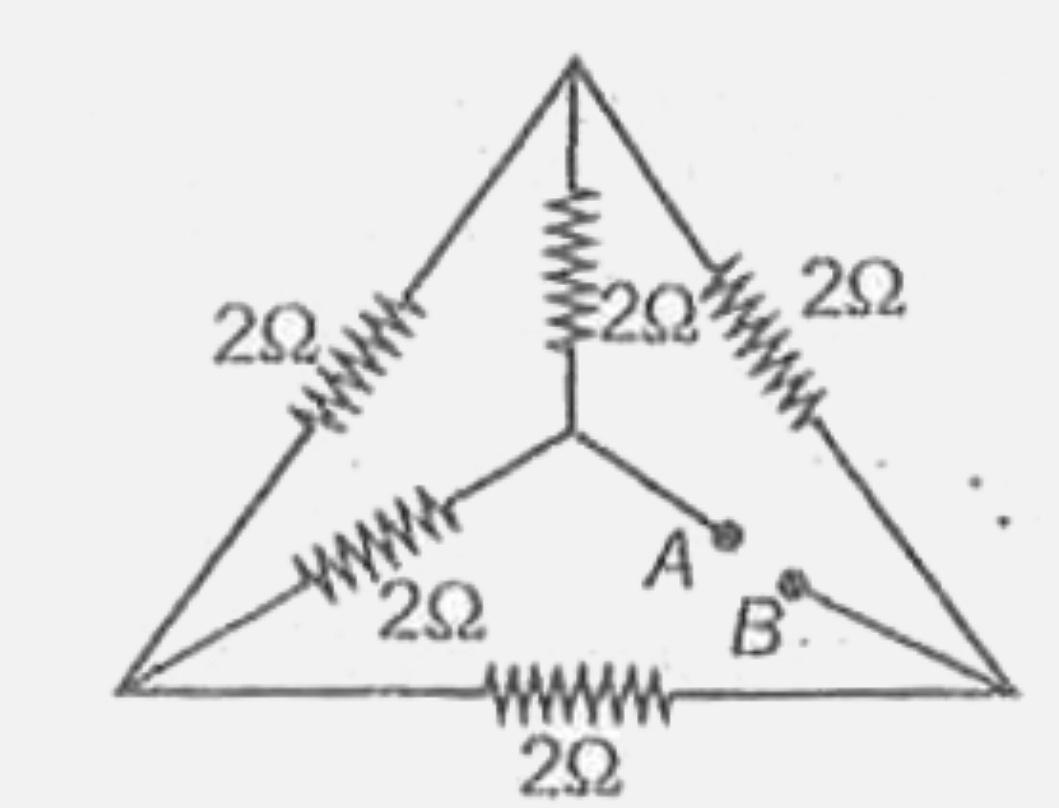
View SolutionFive equal resistances of 10Ω are connected between A and B as shown in figure. The resultant resistance

View Solution
