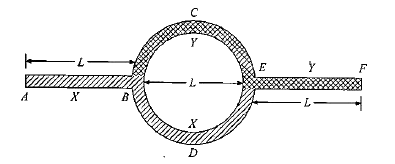
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1C−1 and that of y is 400Wm−1C−1 .
 Solution in Tamil
Solution in Tamil
It is clear from the symmerty of the figure that the points C and D are equivalent in all respect and hence, they are at the same temperature, say (theta). No heat will flow through the rod CD. We can, therefore, neglect this rod in further analysis.
Let l and A be the length and the area of cross section of each rod. The thermal resistances of AB, BC and BD are equal. Each has a value
R1=1KxlA . Similarly, thermal resistances of CE and DE are equal, each having a value
R2=1KylA . As the rod CD has no effect, we can say that the rods BC and CE are joined in sseries. Their equivalent thermal resistance is
R3=RBC+(RCE=R1+R2 . Also, the rods BD and DE together have an equivalent thermal resistance R4=RBD+(RDE=R1+R2 . The resistance R3 and R4 are joined in paralley and hence their equivalent thermal resistance is given by
1R5=1R3+1R4=1R3 . or, =R5=R32=R1+R22 . This resistance R5 is connected in series with AB. Thus, the total arrangement is equivalent to a thermal resistance
R=RAB+R5=R1+R1+R22=3R1+R22 . Figure shows the successive steps in this reduction.
. The heat current through A is
i=θA−θER=2(θA−θE)3R1+R2 . This current passes through the rod AB. We have
i=θA−θBRAB .or, θA−θB=(RAB)i . =R12(θA−θE)3R1+R2 . Putting from (i) and (ii), θA−θB=2Ky(θA−θE)Kx+R2 . =2×400800+3×400×50∘C=20∘C . or, θB=θA−20∘C=40∘C .

Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE I
10 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
55 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
34 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
The heat current is written as ΔQΔt . Why don't we write dQdt ?
View SolutionThe thermal conductivity of a rod depends on
View SolutionA uniform slab of dimension 10cm×10cm×1cm is kept between two heat reservoir at temperatures 10∘C and 90∘C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80Wm−1C−1 . Find the amount of heat flowing through the slab per minute.
View SolutionThe steam point and the ice point of a mercury thermometer are marked as 80∘C and 20∘C. What will be the temperature in centigrade mercury scale when this thermometer reads 32∘C?
View SolutionFind the dimensions of
a. linear momentum
b. frequency and
c. pressure
View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60^@C and the junction E at 10^@C . Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal//sec-cm^@C and that of Y is 0.46cal//sec-cm-^@C .
View SolutionThere rods of material X and there rods of material Y are connected as show in Fig. 7(e).21. All the rods are of identical length and cross-sectional area. If end A is maintained at 60^(@)C and junction E at 10^(@)C , Calculate the temperature of the junctions B,C and D. Given thermal conductivity of X is 0.92 cal cm^(-1) s^(-1) .^(@)C^(-1) and of Y is 0.46 cal cm^(-1) s^(-1) .^(@)C^(-1) .
View SolutionThree rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end A is maintained at 60^(@)C and the junction E at 10^(@0C find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of y =2K .
View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100^(@)C and the other end is kept at 0^(@)C The temperatures of the junctions C,D and E(theta_(D)andtheta_(E)) be in the steady state .
View SolutionA few rods of materials X and Y are connected as shown in The cross-sectional areas of all the rods are same if the end A is maintaind at 80^(@)C and the end F is maintained at 10^(2)C If the temperature of junctions B and E in steady state are (39.48^(@)C)/(n_(1) and (60.52^(@)C)/(n_(2) Find n_(1) and n_(2) Given thermal conductivity of material X double that of Y .
View SolutionThree rods A, B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B , in equilibriu, is
View SolutionTwo rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80^(@)C and the end D is maintained at 10^(@)C , calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y .
View SolutionFour rods of material X and three rods of material Y are connected as shown in figure. All the rods are of identical lengths and cross-sectional area. Given thermal resistance of rod of material X,Rx=R and thermal conductivities of materials are related by relation KY=2KX.
_E01_157_Q01.png)
Column-IColumn-II(A)Thermal resistance between B and E(p)50013.∘C(B)Thermal resistance between A and F(q)70013.∘C(C)Temperature of junction B(r)2R3(D)Temperature of junction D(s)13R6
View SolutionFew rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
View SolutionThree rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
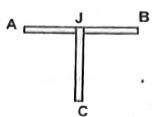
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution
