Three rods of material X and three rods of materail Y are connected as shown in figure. All the rods are of idental length and cross - section areas. If the end A is maintained at 60∘ C and the junction E at 10∘C , calculate the temperature of the junction B, C and D . The thermal conductivity of X is 9.2×10−2 kilocal/m∘C s and that of Y is 4.6×10−2 kilocal/m∘C s.
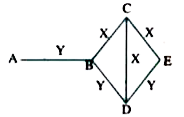
Let θB,θC and θD be the temperature of junction B,C and D respectively at staady state . Let Kx and ky
be thermal conductivites of rods of material X and Y respectively .
The concept in solving the problem is that in steady state heat entering per second at any junction must be equal to that leaving the junction.

As Kx=9.2×10−2
ans Ky=4.6×10−2kilocalm−1(∘C)−1(sec)−1
i.e.., KxKy=9.2×10−24.6×10−22
Let Kx=2K,Ky=K
(or) KyA(60−θB)l=KxA(θB−θC)l+KyA(θB−θC)l
(or) K(60−θB)=2K(θB−θC)+K(θb−θD)∴(60−θB)=2(θB−θC)+θB−θD
∴4θB−2θC−2θD=60...........(1)
For junction C1,H1=H3+H5∴KyA(θB−θC)l=KxA(θc−10)l+kyA(θD−10)l
This gives ∴θB−3θC+θD=−10..........(2)
For junction D, H2+H3=H5∴kyA(θB−θD)l+kyA(θC−θD)l=kyA(θD−10)l
(or) K(θB−θD)+2K(θC−θD)=k(θD−10)
This gives θB+2θC−4θD=−10..............(3) from (2) and (3)
θB−3θC−θD=θB+2θC−4θD
i.e., 5θC=5θD or θC=θD............(4) Substituting this in (1) and (2), we get .
4θB−3θC=60.............(5),θB−2θC=−10............(6)
Solving (5) and (6) , we get θB=30∘C,θC=20∘C
As θc=θD ∴ θC=θD=20∘C
∴ Thus the temperature of junction , B, C and D are 30∘,20∘Cand20∘C respectively.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - TEST YOUR SELF6videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS28videos
TRANSMISSION OF HEAT
- BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)11videos
THERMOMETRY
- BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)3videos
TRANSMISSION OF HEAT
Similar Questions
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
 View Solution
View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three rods of material 'x' and three rods of materialy are connected as shown in All the rods are of identical length and cross section If the end A is maintained at 60∘C and the junction E at 10∘0C find effective Thermal Resistance Given length of each rod =1 area of cross-section =A conductivity of x=K and conductivity of y=2K
 .A4l3KAB7l6KAC4KA3lD7KA3l
.A4l3KAB7l6KAC4KA3lD7KA3l - Question 2 - Select One or More
Seven identical rods of material of thermal conductivity K are connected as shown in figure. All the rods are of identical length L and cross sectional area A1. If one end A is kept at 100∘C and the other end B is kept at 0∘C, what would be the temperature of the junctions C, D and E (TC,TD and TE) in the steady state?
 ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
ATC>TE>TDBTC=TD=37.5∘C,TE=50∘CCTC=62.5∘C,TD=37.5∘C,TE=50∘CDTC=60∘C,TD=40∘C,TE=50∘C
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1C−1 and that of y is 400Wm−1C−1 .
 View Solution
View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .
 View Solution
View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1.∘C−1 and that of y is 400Wm−1.∘C−1 .
 View Solution
View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.
 View Solution
View SolutionTwo rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.
 View Solution
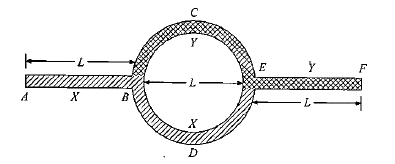
View SolutionFew rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
 View Solution
View Solution

