Twelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
712r
127r
57r
125r
The correct Answer is:A
To find the effective resistance between the corners of the same edge of a cube formed by 12 equal wires each of resistance rΩ, we can follow these steps:
Step 1: Understand the Cube Configuration
The cube has 12 edges, and each edge is represented by a wire with resistance r. We need to find the effective resistance between two corners of one edge, say points D and C.
Step 2: Label the Cube
Label the corners of the cube as follows:
- Bottom face: A,B,C,D
- Top face: E,F,G,H
Step 3: Identify the Current Paths
When a voltage is applied across points D and C, the current can flow through three different paths:
1. Directly from D to C through the edge DC.
2. From D to A to B to C.
3. From D to H to G to C.
Step 4: Analyze Symmetry
Due to the symmetry of the cube, the currents through the paths from D to A to B to C and from D to H to G to C will be equal. Let's denote the current through the direct path DC as I1 and the currents through the other two paths as I2.
Step 5: Apply Kirchhoff's Laws
Using Kirchhoff's Current Law (KCL) at point D:
I=I1+2I2
where I is the total current entering at point D.
Step 6: Apply Kirchhoff's Voltage Law (KVL)
For the loop EFA:
−I1r+I2r+I2r=0
This simplifies to:
−I1+2I2=0⇒I1=2I2
Step 7: Substitute Back into KCL
Substituting I1=2I2 into the KCL equation:
I=2I2+2I2=4I2⇒I2=I4
Thus, I1=2I2=2⋅I4=I2.
Step 8: Calculate the Effective Resistance
The total resistance Rtotal can be calculated using the formula for resistors in parallel and series:
- The resistance of the direct path DC is r.
- The two paths through A and H are in parallel, each having resistance 2r (two resistors of r in series).
Using the formula for resistors in parallel:
1Rparallel=12r+12r=22r=1r⇒Rparallel=r
Step 9: Combine the Resistances
Now, the effective resistance Reff between points D and C is:
Reff=RDC+Rparallel=r+r=2r
Final Result
The effective resistance between the corners of the same edge of the cube is:
7r12
The cube has 12 edges, and each edge is represented by a wire with resistance r. We need to find the effective resistance between two corners of one edge, say points D and C.
Label the corners of the cube as follows:
- Bottom face: A,B,C,D
- Top face: E,F,G,H
When a voltage is applied across points D and C, the current can flow through three different paths:
1. Directly from D to C through the edge DC.
2. From D to A to B to C.
3. From D to H to G to C.
Due to the symmetry of the cube, the currents through the paths from D to A to B to C and from D to H to G to C will be equal. Let's denote the current through the direct path DC as I1 and the currents through the other two paths as I2.
Using Kirchhoff's Current Law (KCL) at point D:
I=I1+2I2
where I is the total current entering at point D.
For the loop EFA:
−I1r+I2r+I2r=0
This simplifies to:
−I1+2I2=0⇒I1=2I2
Substituting I1=2I2 into the KCL equation:
I=2I2+2I2=4I2⇒I2=I4
Thus, I1=2I2=2⋅I4=I2.
The total resistance Rtotal can be calculated using the formula for resistors in parallel and series:
- The resistance of the direct path DC is r.
- The two paths through A and H are in parallel, each having resistance 2r (two resistors of r in series).
1Rparallel=12r+12r=22r=1r⇒Rparallel=r
Now, the effective resistance Reff between points D and C is:
Reff=RDC+Rparallel=r+r=2r
The effective resistance between the corners of the same edge of the cube is:
7r12
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NIKITA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Multiple Choice Questions
314 Videos
- COMMUNICATION SYSTEMSBOOK - NIKITA PUBLICATIONCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Multiple Choice Questions (Examples for Practice)
8 Videos
- ELASTICITYBOOK - NIKITA PUBLICATIONCHAPTER - ELASTICITYEXERCISE - MCQ
314 Videos
Similar Questions
Twelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View SolutionA wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
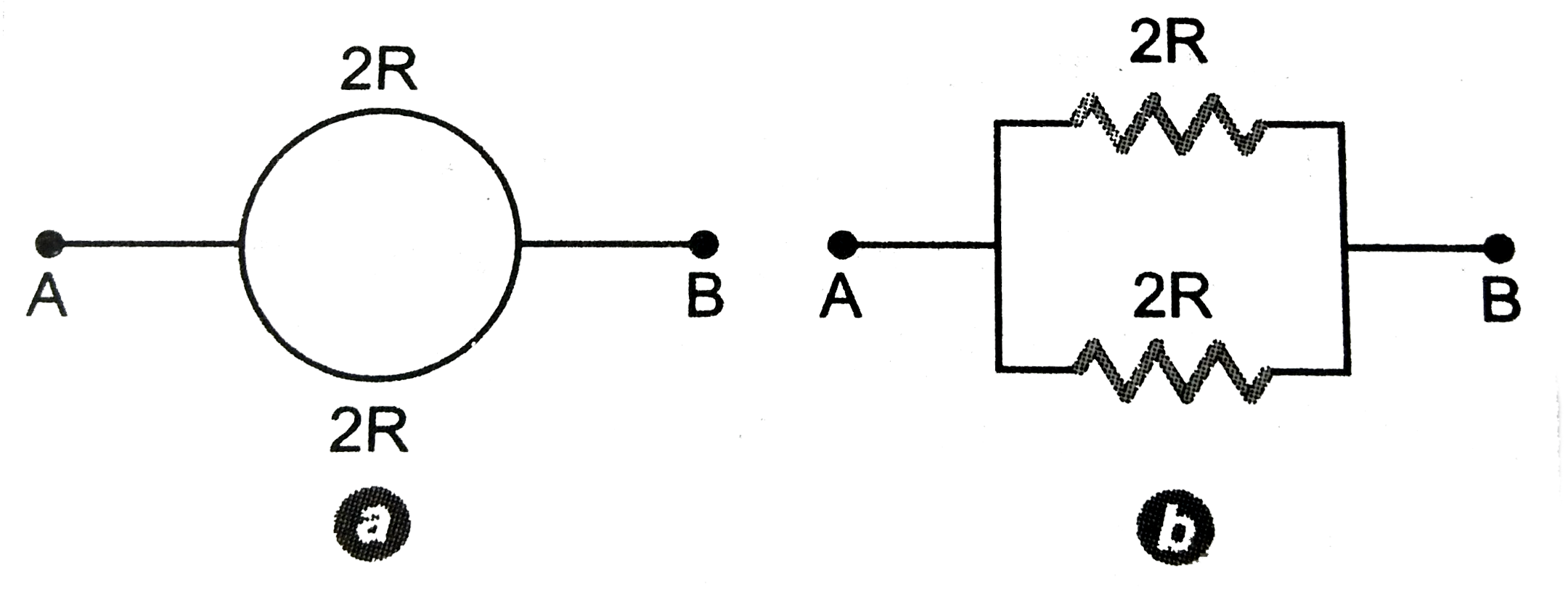
View Solution
Knowledge Check
Twelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩA uniform wire of resistance 2R is bent in the form of a circle. The effective resistance between the ends of any diameter of the circle is
A2RBRCR2DR4Six wires each of resistance r form a tetrahedron. The equivalent resistance between corners 1-2 and 1-3 are respectively
 Ar2,r2Br, rCr2,rDr,r2
Ar2,r2Br, rCr2,rDr,r2
A wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
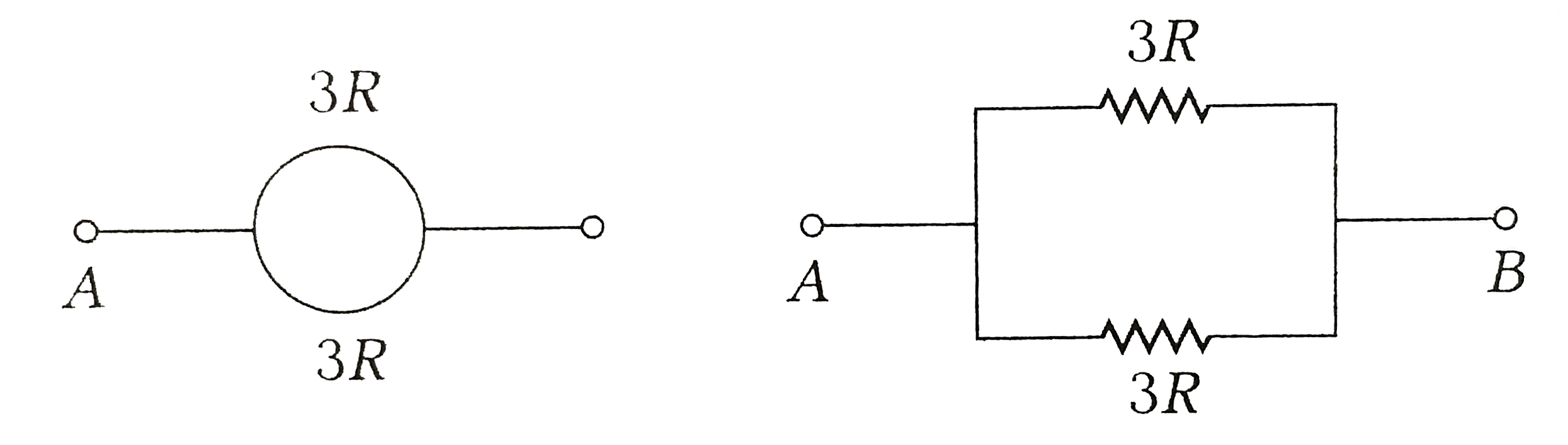
View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB ?
View SolutionTwelve resistors of equal value R are connected in the form of a cube. Effective resistance between diagonals of the cube is

View Solution