Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
32V
53V
35V
2V
The correct Answer is:B
To find the effective EMF of two batteries connected in parallel, we can follow these steps:
1. Identify the given values:
- For Battery 1:
- EMF (E1) = 2 V
- Internal Resistance (R1) = 1 Ω
- For Battery 2:
- EMF (E2) = 1 V
- Internal Resistance (R2) = 2 Ω
2. Use the formula for effective EMF in parallel:
The formula for the effective EMF (E_effective) when two batteries are connected in parallel is given by:
Eeffective=E1R2+E2R1R1+R2
3. Substitute the values into the formula:
Eeffective=(2V⋅2Ω)+(1V⋅1Ω)1Ω+2Ω
4. Calculate the numerator:
- Calculate 2V⋅2Ω=4V⋅Ω
- Calculate 1V⋅1Ω=1V⋅Ω
- Therefore, the numerator becomes:
4V⋅Ω+1V⋅Ω=5V⋅Ω
5. Calculate the denominator:
- R1+R2=1Ω+2Ω=3Ω
6. Combine the results:
Eeffective=5V⋅Ω3Ω=53V
7. Final Result:
The effective EMF of the combination is:
Eeffective=53V
Conclusion:
The effective EMF of the combination of the two batteries connected in parallel is 53V.
- For Battery 1:
- EMF (E1) = 2 V
- Internal Resistance (R1) = 1 Ω
- For Battery 2:
- EMF (E2) = 1 V
- Internal Resistance (R2) = 2 Ω
The formula for the effective EMF (E_effective) when two batteries are connected in parallel is given by:
Eeffective=E1R2+E2R1R1+R2
Eeffective=(2V⋅2Ω)+(1V⋅1Ω)1Ω+2Ω
- Calculate 2V⋅2Ω=4V⋅Ω
- Calculate 1V⋅1Ω=1V⋅Ω
- Therefore, the numerator becomes:
4V⋅Ω+1V⋅Ω=5V⋅Ω
- R1+R2=1Ω+2Ω=3Ω
Eeffective=5V⋅Ω3Ω=53V
The effective EMF of the combination is:
Eeffective=53V
The effective EMF of the combination of the two batteries connected in parallel is 53V.
Topper's Solved these Questions
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:CHECK YOUR NEET VITALS
Explore 16 Videos
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:MCQs AIPMT / NEET
Explore 32 Videos
- CURRENT ELECTRICITY Book:MTG GUIDEChapter:CURRENT ELECTRICITY Exercise:MCQs AIPMT / NEET
Explore 32 Videos
- ATOMS AND NUCLEIBook:MTG GUIDEChapter:ATOMS AND NUCLEIExercise:AIPMT/NEET(MCQs)
Explore 40 Videos
- DUAL NATURE OF MATTER AND RADIATION Book:MTG GUIDEChapter:DUAL NATURE OF MATTER AND RADIATION Exercise:AIPMT/ NEET MCQs
Explore 30 Videos
Similar Questions
Three batteries of emf 4,5 and 6V and internal resistances 1,2 and 3Ω respectively are connected in parallel with each other and the combination sends a current through an external resistance of 4Ω. Find current drawn through each battery.
View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View Solution
Knowledge Check
Two cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
A0.87 AB1.29 AC1.00 AD2.29 ATwo cells of emf 1.25V,0.75V and each of internal resistance 1Ω are connected in parallel. The effective emf will be
A1 VB1.25 VC2 VD0.5 V
Two cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo batteries of emfs 24V and 6V and internal resistance 2Ω and 1Ω respectively are joined in parallel, negative to negarive by a resistor of 2Ω and positive to positive by another resistor of 4Ω. Calculate the terminal voltages of the two batteries.
View SolutionTwo cells of voltage 10Vand 2V and internal resistance 10Ω and 5Ω respectively , are connected in parallel with the pesition and of 10V battery connected to negative pole of 2V battery Find the effected voltage and effected resistance of the combination
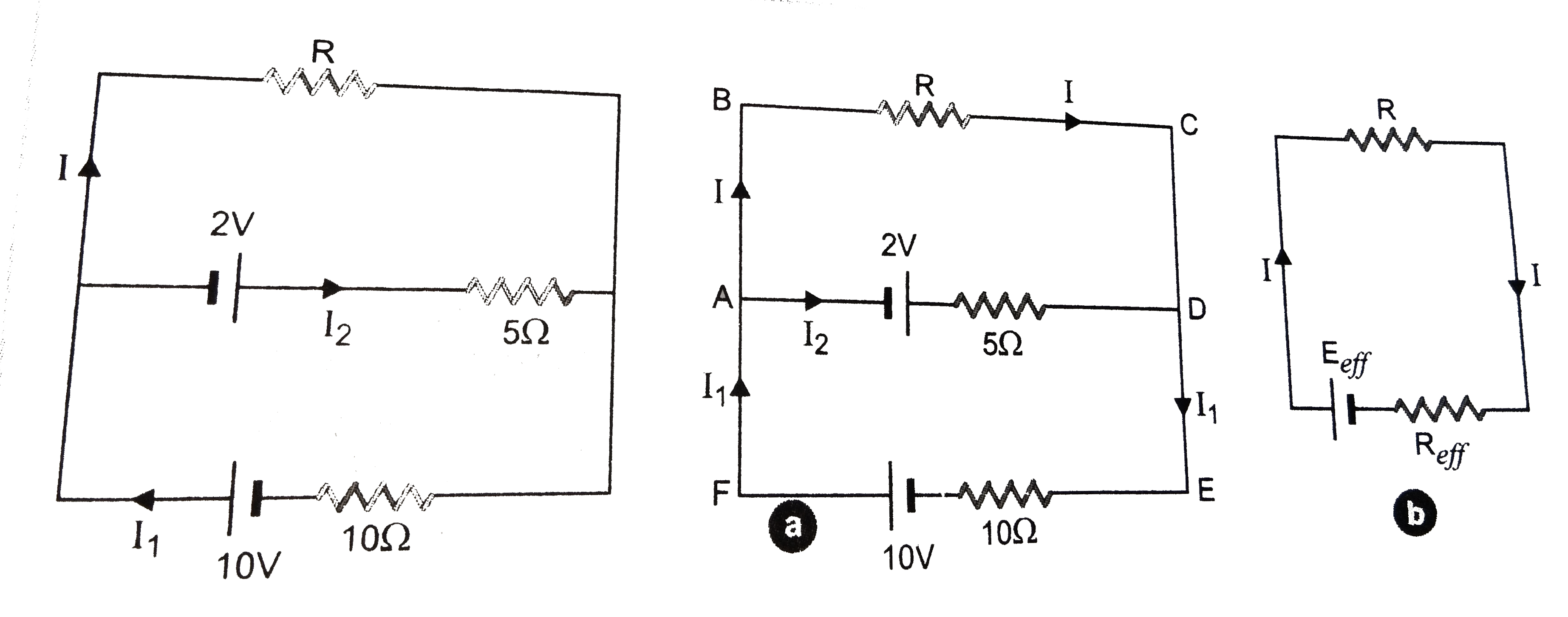
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionTwo batteries of emf 12V and 6V and internal resistance 2Ω and 1Ω are connected in parallel and the combination is connected to a resisor of 2Ω through a key. Find the potential difference between the positive and negative terminals of the batteries (a) When key is open, b) when key is closed. Find the emf and internal resistance of a single cell which would be equivalent to the combination.
View SolutionTwo cells, of voltage 10 V and 2 V and internal resistances 10Ω and 5Ω respectively, are connected in parallel as shown in Fig. Find the effective voltage and effective resistance of the combination.
View Solution
