Two beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

If m2 again comes down and collides with m1 then after the collision
m1 will rise the same height as risen by m2
m1 will rise the less height as risen by m2
m1 will rise the more height as risen by m2
m1 and m2 will move in opposite directions
The correct Answer is:A
m1v1+m2v2=m2u2
⇒m1v1+√2m1v2=√m1u2
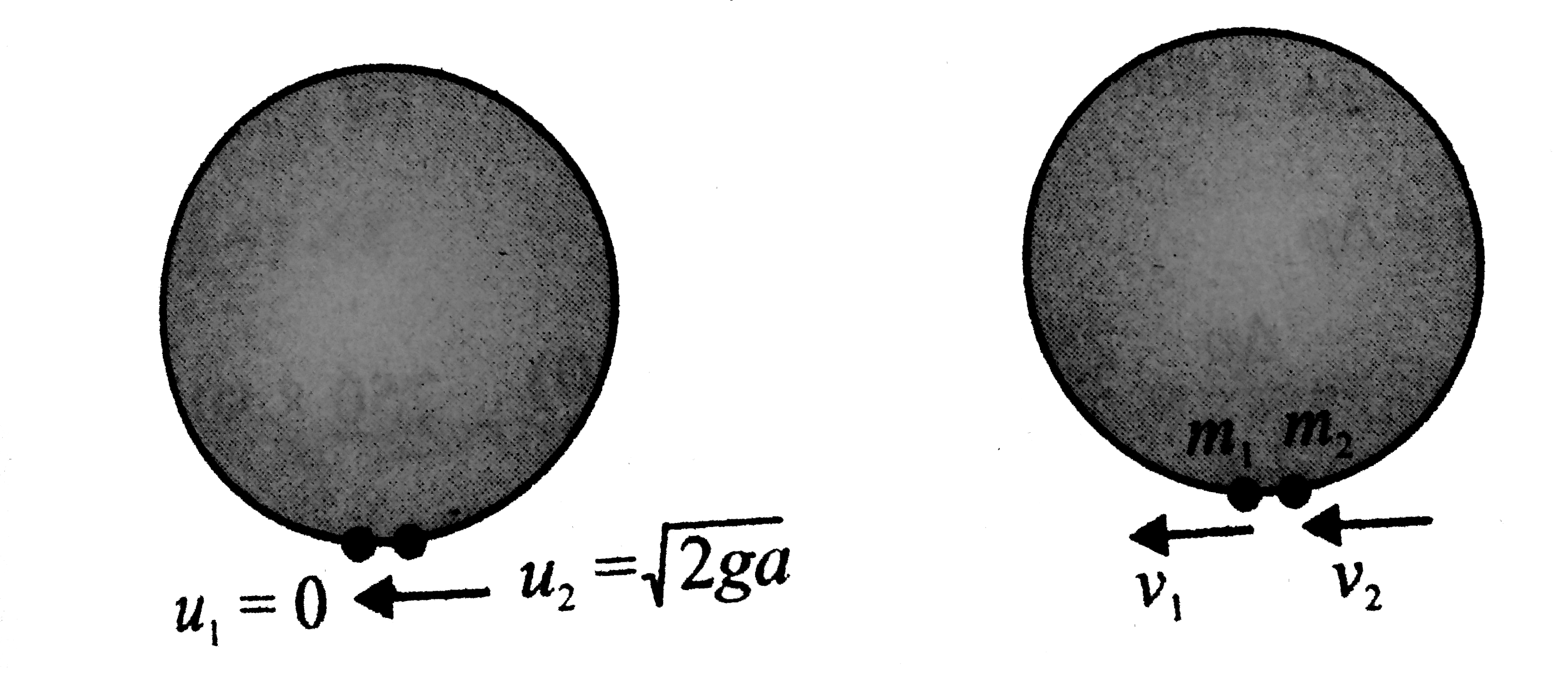
⇒v1+√2v2=√2u2
e=1√2=v1−v2u2−u1⇒1√2=v1−v2u2
⇒v1−v2=u2√2…………..ii
Solving eqn i and ii we get v1=u2=√2ga
Both are positive so both move same direction. height raised by m1,
v212g=a, same as that of m2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

Find the ratio m1:m2View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?View Solution
What is the coefficient of restituting between the beads?View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View SolutionTwo balls A & B of mass m1 and m2 are kept on a horizontal smooth surface. A is given a velocity towards B so that they perform head on collision
View SolutionTwo satellites , A and B , have masses m and 2m respectively . A is in a circular orbit of radius R , and B is in a circular orbit of radius 2R around the earth . The ratio of their energies , KAKB is :
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
 .View Solution
.View SolutionThe maximum velocity at the lowest point, so that the string just slack at the highest point in a vertical circle of radius l.
View SolutionTwo satellites, A and B, have masses m and 2m respectively. A is in a circular orbit of radius R, and B is in a circular orbit of radius 2R around the earth. The ratio of their kinetic energies, TA/TB, is :
View SolutionA smooth circular tube of radius R is fixed in a vertical plane. A particle is projectid from its lowest point with a velocity just sufficient to carry it to th ehigest point. Show that the time taken by the particle to rach the end of the horizontal diameter is (√Rg)In(1+√2) .
Hint : ∫secθ.dthη=In(secθ+tanθ)View SolutionA section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block id released from position A and leaves the treack at B The radius of curvanture of its trajectory just after it leaves the track B is ?
 View Solution
View Solution

