Two blocks are floating in water. When they are brought sufficiently close they are attracted to each other due to surface tension effects. When the experiment is repeated after replacing water with mercury, once again the two blocks are attracted. Explain the phenomena. It is given that water wets the material of the block where as mercury does not.
Step by step video, text & image solution for Two blocks are floating in water. When they are brought sufficiently close they are attracted to each other due to surface tension effects. When the experiment is repeated after replacing water with mercury, once again the two blocks are attracted. Explain the phenomena. It is given that water wets the material of the block where as mercury does not. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two blocks each of mass m are placed on a smooth horizontal surface.They attract each other with a force F=kr where r is the separation between them.Calculate work required to increase the separation between the blocks slowly from a to 2a.
View Solution(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View Solution
Knowledge Check
Two blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
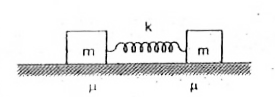 A2μmg/kBμmg/kCzeroDnot possible
A2μmg/kBμmg/kCzeroDnot possibleTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
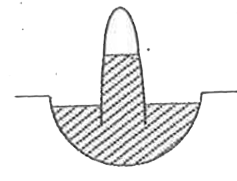
If this expriment uses water instead of mercury , thenAlength of water will be equal to 76 cmBlength of water will be less than 76 cmClength of water will be greater than 76 cmDnone of the aboveTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
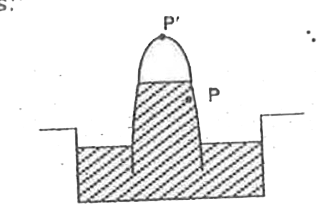
If an additional hole is also made at P ' at the top point of the tube , then
 Amercury will not come out of the tubeBmercury may come out of the tube after some time .Cmercury will come out of the tube instantlyDnone of these
Amercury will not come out of the tubeBmercury may come out of the tube after some time .Cmercury will come out of the tube instantlyDnone of these
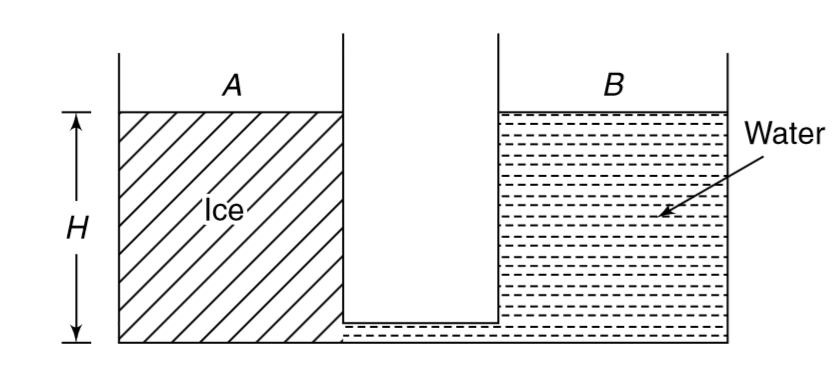
Two identical cylindrical containers A and B are interconnected by a tube of negligible dimensions. Container A is filled with an ice block up to height H = 1.8 m and container B is filled up to same height with water. Ice is at 0∘C and water is at 40∘C. Due to heat exchange between water and ice, the ice block begins to melt. Assume that the ice block melt in horizontal layers starting from the bottom. The thickness of ice block reduces uniformly over the entire cross section of the container. The ice block moves without friction inside the container and no water enters between the vertical wall of the container and the ice block. Heat is exchanged only between the ice block and the water and there is no heat exchange with containers or atmosphere. Calculate the height of water in container B when thermal equilibrium is attained. Relative density and specific latent heat of fusion of ice are 0.9 and 80calg−1 respectively. Specific heat capacity of water is 1calg−1.∘C−1.
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mrcury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If a small hole is made at point P in the barometer tube , then
View SolutionWhen liquid medicine ρ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop froms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is osperical becaus ethat requires a minimum increase in its surface energy. To datermine the size., we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force become smaller than the wight of the drop, the drop gets detached from the droppr.
A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different raddi. When dipped in water verically, water rises in it to a height h, where the radius of its cross section is b. If the surface tension of water is S, its density is ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)

View SolutionNegative Refractive Index:
One of the most fundamental phenomena in optics is refraction. When a beam of light crosses the interface between two different materials, its path is altered depending on the difference in the refractive indices of the materials. The greater the difference, the greater the refraction of the beam. For all known naturally occurring materials the refractive index assumes only positive values. But does this have to be the case?
In 1967, Soviet physicist Victor Veselago hypothesized that a material with a negative refractive index could exist without violating any of the laws of physics.
Veselago predicted that this remarkable material would exhibit a wide variety of new optical phenomena. However, until recently no one had found such a material and Veselago's ideas had remained untested. Recently, meta-material samples are being tested for negative refractive index. But the experiments show significant losses and this could be an intrinsic property of negative index materials.
Snell's law is satisfied for the material having a negative refractive index, but the direction of the refracted light ray is 'mirror-imaged about the normal to the surface.

There will be an interesting difference in image formation if a vessel is filled with "negative water" having refractive index - 1.33 instead of regular water having refractive index 1.33.
Say, there is a fish in a vessel filled with negative water. The position of the fish is such that the observer cannot see it due to normal refraction since the refracted ray does not reach to his eye.
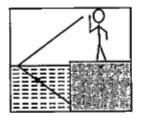
But due to negative refraction, he will be able to see it since the refracted ray now reaches his eye.
When the angle of incidence will be equal to angle of refraction for material having negative refraction index?
View Solution
