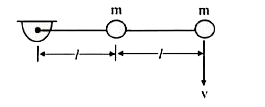
Two blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.

(ml2g−ml1g)ˆk
(ml1g−ml2g)ˆk
(ml1g+ml2g)ˆk
−(ml1g+ml2g)ˆk
The correct Answer is:B
Torque due to weight of left m
→τ1=mgl1ˆk(this is anticlockwise)
Torque due to weight of right m
→τ2=−mgl2ˆk(this is clockwise)
So net torque →τ=→τ+→τ2=(mgl1−mgl2)ˆk
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Two masses each of m are attached at mid point B and end point C of massless rod AC which is hinged at A. It is released from horizontal position as shown. Find the force at hinge A when rod becomes vertical.
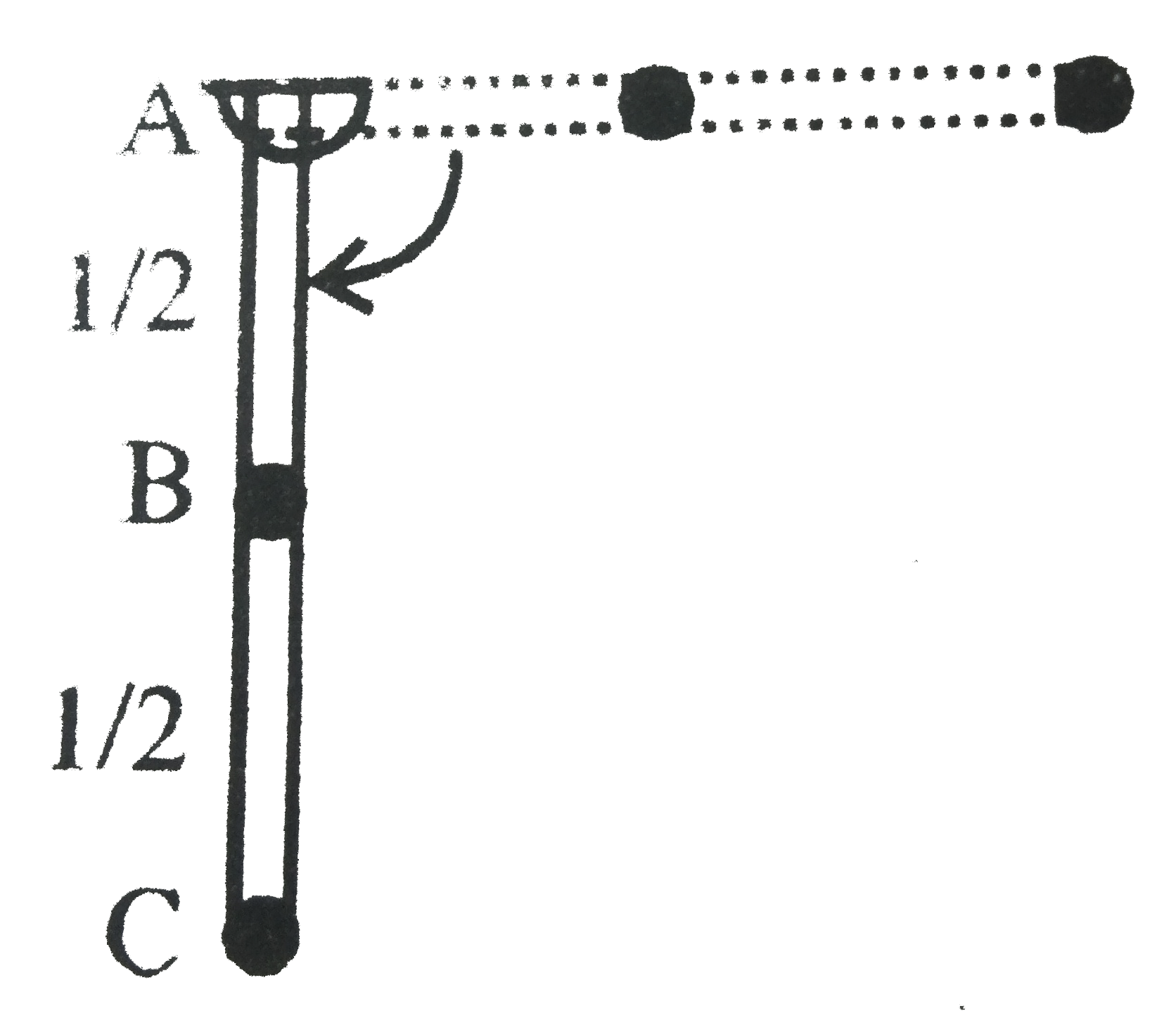 .
.
View SolutionA rod of mass M is hanged at one end at the other end, a block of same mass M is attached rigidly. The rod is held at in horizontal position and is suddenly released. The angular acceleration of the system about O is xg/(8l) then the value of X.
View Solution
Knowledge Check
Two blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.
 A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwise
A(l2−l1)gl21+l22 clockwiseB(l2+l1)g(l22+l21) clockwiseC(l2−l1)g2(l22+l21) clockwiseDgl2+l1 clockwiseTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
 ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zeroA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3
Two beads each of mas m are fixed at the ends of two light rigid rods each of length l as shown in the figure. If the pivot is smooth. Calculate the ratio of translational and rotational kinetic energy of system.
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is

View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)

View SolutionA ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vertical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The initial speed given to the ball is

View Solution
