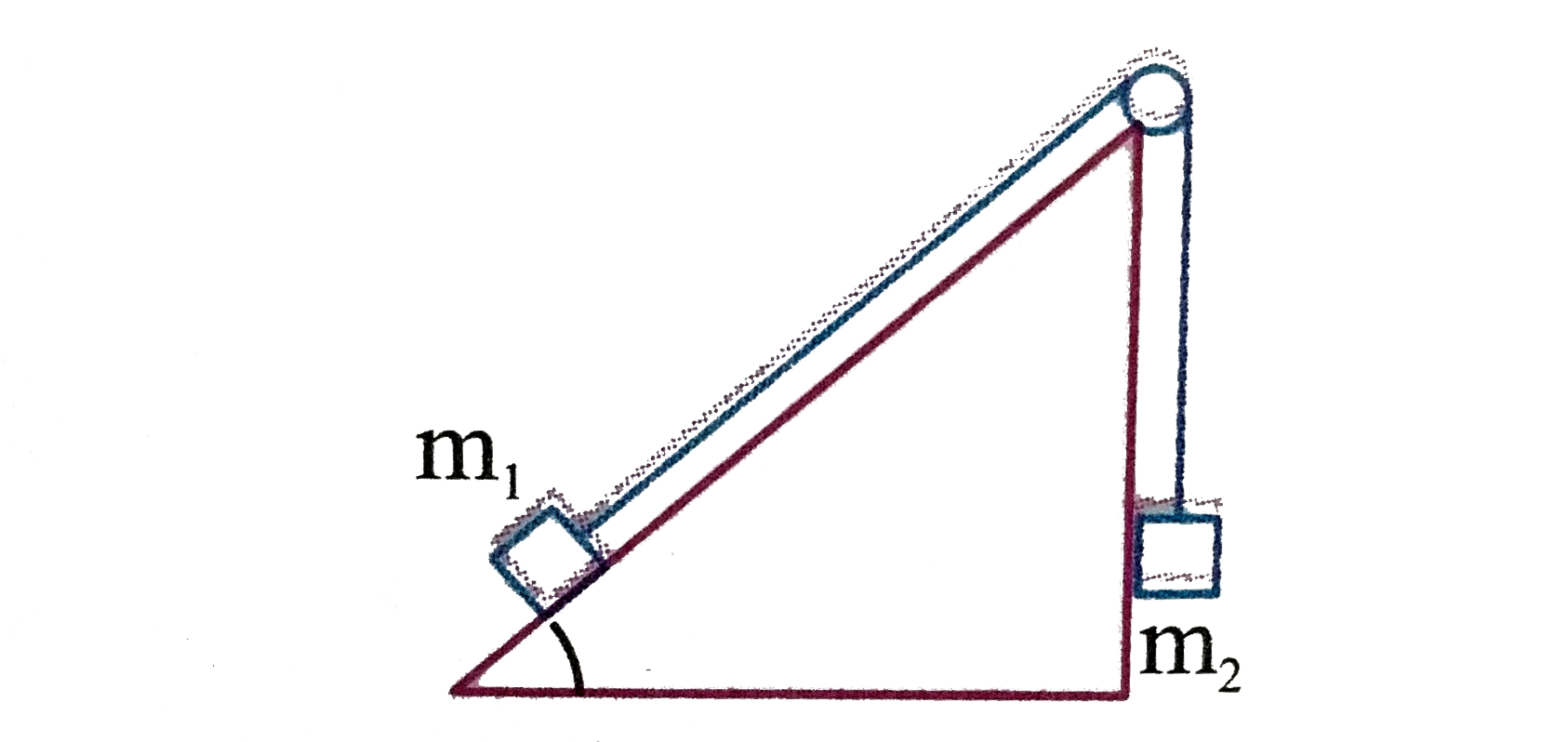
Two blocks of mass m and M, are connect to the ends of a string passing over a pulley. M lies on the plane inclined at an angle θ with the horizontal and m is hanging vertically as shown in Fig. The coefficient of static friction between M and the incline is μs. Find the minimum and maximum value of m so that the system is at rest.

In the present problem motion will depend on the relative values of m and M . If m is heavier than M , then the block M will move upwards . If m is much lighter than M , then the block M will move downwards .

Consider following situations :
Case (i) : M is about to start sliding upwards (Motion impending upwards) . This will happen if m is much heavier than M .
As M is just at the point of sliding up , frictional force on M is μsN acting down the plane .
Balancing forces along x-axis and y-axis :
NMg cosθ,T=Mg sinθ+μsN,T=mg
Hence , mg=Mg sinθ+μsMg cosθ
Maximum value of m = M(sinθ+μscosθ)
Case (ii) : M is about to start sliding downwards (motion impending downwards) . This will happen if m is much lighter than M .

As M is about to start sliding down , the frictional force is μsN acting upwards .
Balancing forces along x-axis and y-axis :
N=Mg cosθ,T=Mg sinθ−μsN,T=mg
Hence , mg = Mg sin θ−μsMg cosθ

Minimum value of m = M (sin θ−μscosθ)
Therefore the blocks are at rest if ,
M (sin θ−μscosθ)<m<M(sinθ+μscosθ)
Related Playlists
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice23videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )80videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Knowledge Check
- Question 1 - Select One
In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2 - Question 1 - Select One
Two block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?
 AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ - Question 1 - Select One
In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is
 AM=μm2Bm=μM2CM=m2μDm=M2μ
AM=μm2Bm=μM2CM=m2μDm=M2μ - Question 1 - Select One
An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
AmgsinθBμmgcosθCμmgcosθ−mgsinθDμmgcosθ+mgsinθ - Question 1 - Select One
Two blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest
 A4/3kgB8/9kgC1kgD8/5kg
A4/3kgB8/9kgC1kgD8/5kg - Question 1 - Select One or More
Two blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
 AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
Similar Questions
Two blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.
 View Solution
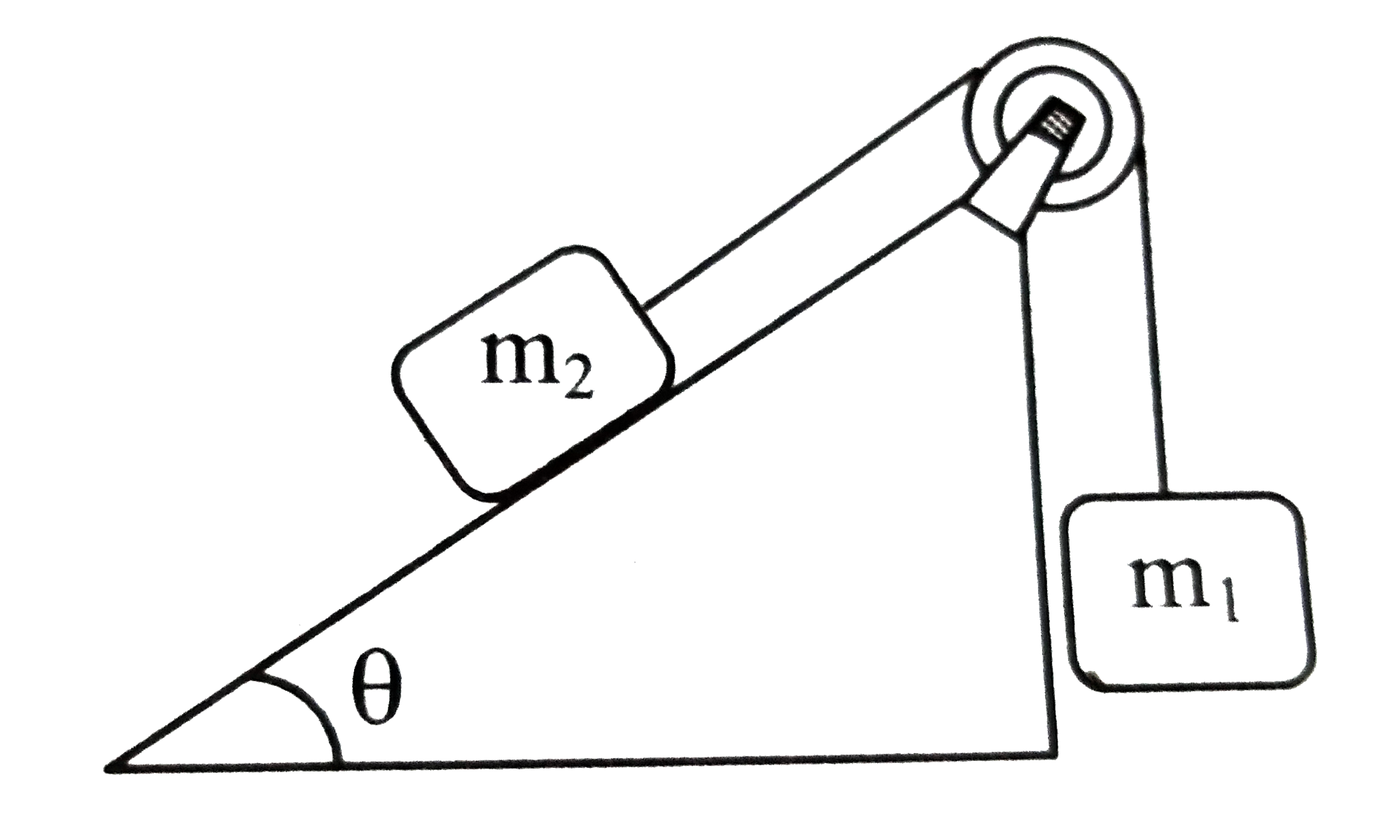
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
 View Solution
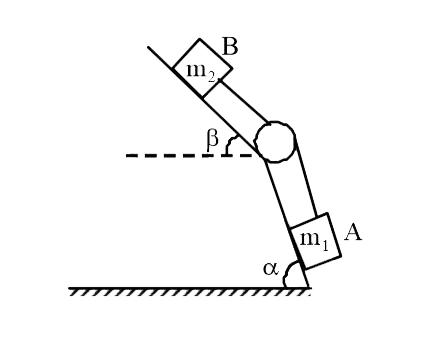
View SolutionTwo blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
 View Solution
View SolutionIf the coefficient of friction between M and the inclined surfaces is μ=1/√3 find the minimum mass m of the rod so that the of mass M=10kg remain stationary on the inclined plane
 View Solution
View Solution

