Two blocks of masses m1=2kg and m2=4kg are moving in the same direction with speeds v1=6m/s and v2=3m/s, respectively on a frictionless surface as shown in the figure. An ideal spring with spring constant k=30000N/m is attached to the back side of m2. Then the maximum compression of the spring after collision will be
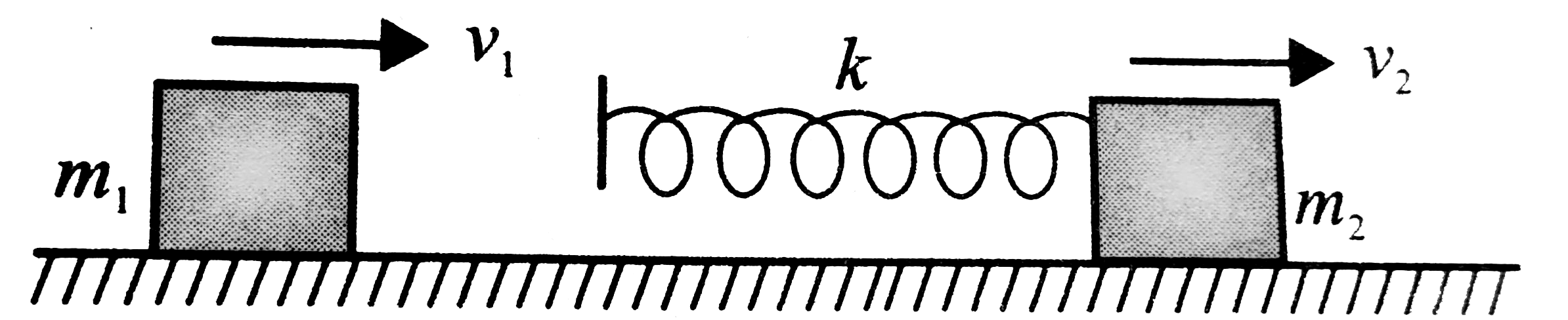
0.06m
0.04m
0.02m
none of these
The correct Answer is:C
At the time of maximum compression, the speeds of blocks will be the same. Let the speed be v and maximum compression be x.
Applying conservation of momentum,
(m1+m2)v=m1v1+m2v2
⇒V=4m/s Applying conservation of mechanical energy,
12kx2+12(m1+m2)v2=12m1v22+12m2v22
solving we get x=0.02m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two blocks of masses m1=2kg and m2=5 kg are moving in the same direction along a frictionless surface with speeds 10m/s and 3m/s, respectively, m2 being ahead of m1. An ideal spring with k=1120N/m is attached to the back side of m2. Find the maximum compression of the spring when the blocks collide. What are the final velocities of the blocks when they separate?
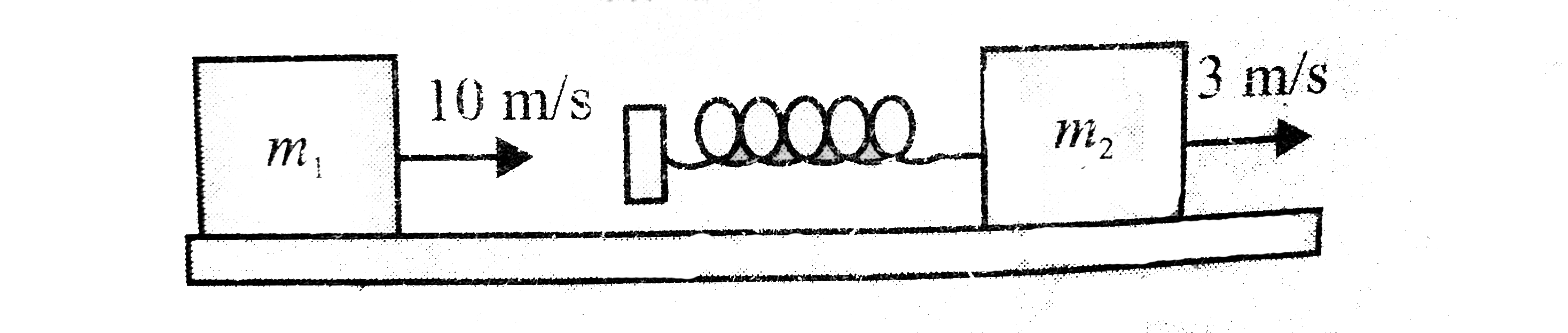 View Solution
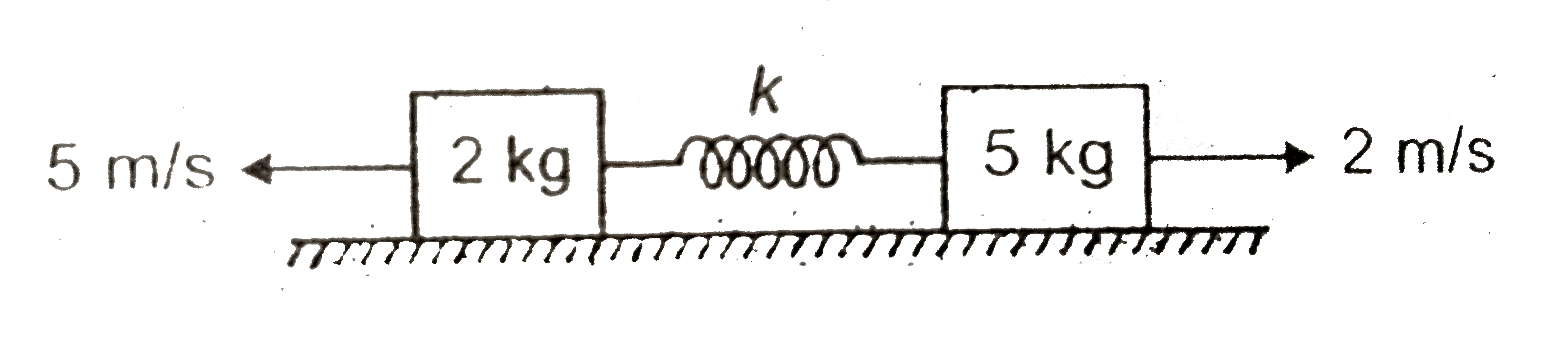
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
 A5cmB2cmC3cmD4cm
A5cmB2cmC3cmD4cm - Question 2 - Select One
A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
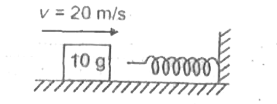 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43m - Question 3 - Select One
The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 AkL22MB√MkL(c)SCML2kDzero
AkL22MB√MkL(c)SCML2kDzero

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)View SolutionA body of mass M is moving on a smooth surface with speed v0. Another body of same mass M attached to a spring is kept on the same surface as shown. The moving mas makes an impact with the spring of spring constant k and starts compressing it. What is the maximum compression in the spring ?
 View Solution
View SolutionA block of mass m1 =2 kg slides along a firictionless table with a speed of 10m/s. Directly infront of it,and moving in the same direction is a block of mass m2 5 kg moving at 3 m/s. A mass less spring with a spring constant 11.2 N/cm is attached to as shown in figure-5.146. When the block collide,what is the maximum compression of the spring ? Assume that the spring does not bend.
 View Solution
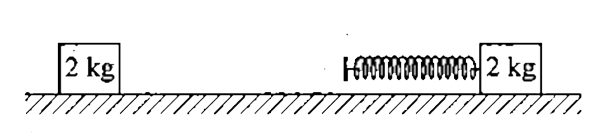
View SolutionA block of mass 2 kg is moving on a frictionless horizontal surface with a velocity of 1m/s towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100N/m. Find the rnaximum compression of the spring
 View Solution
View Solutionmass of 0.5 kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be
 View Solution
View Solution

