Two blocks of masses m1 = 3 kg and m2=1√3 kg are connected by a light inextensible string which passes over a smooth peg . The blocks rest on the inclined smooth planes of a wedge and the peg is fixed to the top of the wedge . The planes of the wedge supporting m1 and m2 are inclined at 30∘ and 60∘ respectively , with the horizontal. Calculate the acceleration of masses and the tension in the string .
As m1gsin30∘>m2gsin60∘ , so m1 will be moving downward and m2 upward with the same acceleration as the string is inextensible . The forces and their resolved

components along and perpendicular to the incline are shown in Fig . 7.57 . The equations of motion are :
m1gsin30∘−T=m1a .......(i)
T−m2gsin60∘=m2a ....(ii)
Adding and solving ,
a=m1gsin30∘−m2gsin60∘(m1+m2)
(3×12−1√3×√32)×10(3+1√3)
= 2.8m/s2
Substituting for a in eqn .(i)
T=m1gsin30∘−m1a
=3×10×12−3×2.8
=6.6N
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
Two blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
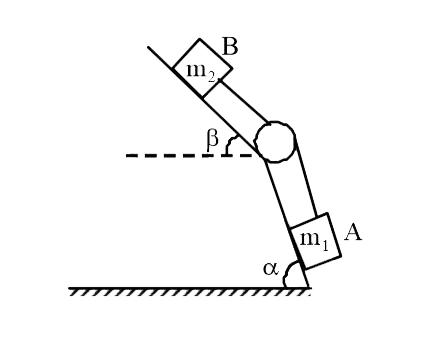
View SolutionTwo smooth blocks of masses m and m' connected by a light inextensible strings are moving on a smooth wedge of mass M. If a force F acts on the wedge the blocks do not slide relative to the wedge. Find the (a) acceleration of the wedge and (b) value of F.

View Solution
Knowledge Check
Two blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
A(m2−m1m1+m2)gB(m1+m2m1−m2)gC(m1+m2m1−m2)gD(m1−m2m1+m2)2gTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
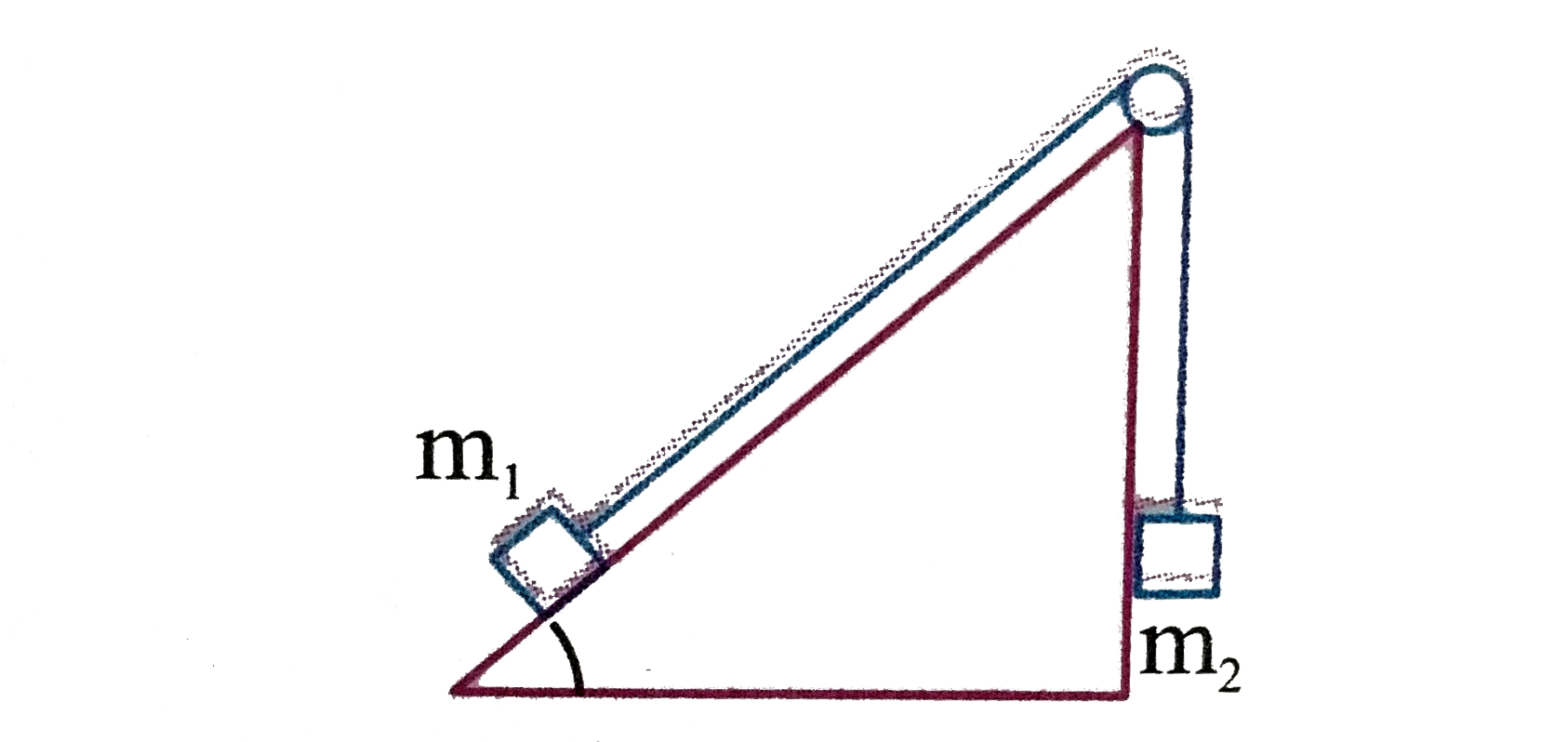 AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.Two block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?
 AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
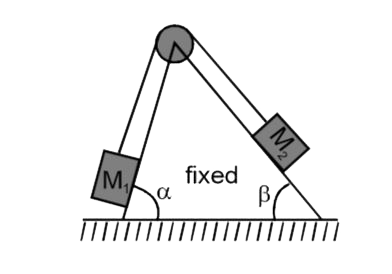
View SolutionTwo blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles 30∘ and 60∘ resp . With horizontal .Determine the accelertion in the two blocks and tension in the string g=10m/s2 .
View SolutionA body of mass 50kg resting on a smooth inclined plane is connected by a massless inextensible string passing over a smooth pulley, at the top of the inclined plane have another mass of 40 kg as shown in the figure. The distance through which 50 kg mass fall in 4 sec will be - (The angle of the inclined plane is 30∘)

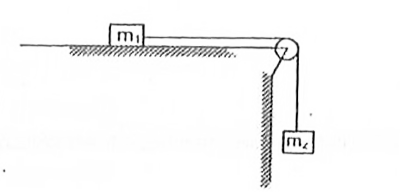
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionThree blocks are placed at rest on a smooth inclined plane with force acting on m1 parallel to the inclined plane. Find the contact force between m2 and m3

View Solution