Two blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles 30∘ and 60∘ resp . With horizontal .Determine the accelertion in the two blocks and tension in the string g=10m/s2 .
To solve the problem, we will analyze the forces acting on each block and apply Newton's second law. Here are the steps to find the acceleration of the blocks and the tension in the string.
Step 1: Identify the forces acting on each block
1. For Block 1 (mass = 30 kg, inclined at 60°):
- Weight (mg) acting downward: W1=30×g=30×10=300N
- The component of weight acting down the incline: W1x=W1sin(60°)=300sin(60°)=300×√32=150√3N
- Tension (T) acting up the incline.
2. For Block 2 (mass = 50 kg, inclined at 30°):
- Weight (mg) acting downward: W2=50×g=50×10=500N
- The component of weight acting down the incline: W2x=W2sin(30°)=500sin(30°)=500×12=250N
- Tension (T) acting up the incline.
Step 2: Write the equations of motion for each block
1. For Block 1 (30 kg):
T−150√3=−30a(1)
Here, the negative sign indicates that the block is accelerating down the incline.
2. For Block 2 (50 kg):
250−T=50a(2)
Step 3: Solve the equations simultaneously
From equation (1):
T=150√3−30a(3)
Substituting equation (3) into equation (2):
250−(150√3−30a)=50a
250−150√3+30a=50a
250−150√3=50a−30a
250−150√3=20a
a=250−150√320
Step 4: Calculate the value of acceleration (a)
Using √3≈1.732:
a=250−150×1.73220
a=250−259.820
a=−9.820=−0.49m/s2
Step 5: Calculate the tension (T)
Substituting the value of a back into equation (3):
T=150√3−30(−0.49)
T=150×1.732+14.7
T=259.8+14.7=274.5N
Final Results
- The acceleration of the blocks is approximately −0.49m/s2 (indicating the direction of motion).
- The tension in the string is approximately 274.5N.
- Weight (mg) acting downward: W1=30×g=30×10=300N
- The component of weight acting down the incline: W1x=W1sin(60°)=300sin(60°)=300×√32=150√3N
- Tension (T) acting up the incline.
- Weight (mg) acting downward: W2=50×g=50×10=500N
- The component of weight acting down the incline: W2x=W2sin(30°)=500sin(30°)=500×12=250N
- Tension (T) acting up the incline.
T−150√3=−30a(1)
Here, the negative sign indicates that the block is accelerating down the incline.
250−T=50a(2)
T=150√3−30a(3)
250−(150√3−30a)=50a
250−150√3+30a=50a
250−150√3=50a−30a
250−150√3=20a
a=250−150√320
a=250−150×1.73220
a=250−259.820
a=−9.820=−0.49m/s2
T=150√3−30(−0.49)
T=150×1.732+14.7
T=259.8+14.7=274.5N
- The acceleration of the blocks is approximately −0.49m/s2 (indicating the direction of motion).
- The tension in the string is approximately 274.5N.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - conceptual problmes45videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer questions73videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of mass 2 kg and 5 kg are connected by an ideal string passing over a pulley. The block of mass 2 kg is free to slide on a surface inclined at an angle of 30∘ with the horizontal whereas 5 kg block hangs freely. Find the acceleration of the system and the tension in the string. Given μ=0.30.
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2 - Question 2 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A188 NB2=368 NC288 ND168 N
A188 NB2=368 NC288 ND168 N - Question 3 - Select One
Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
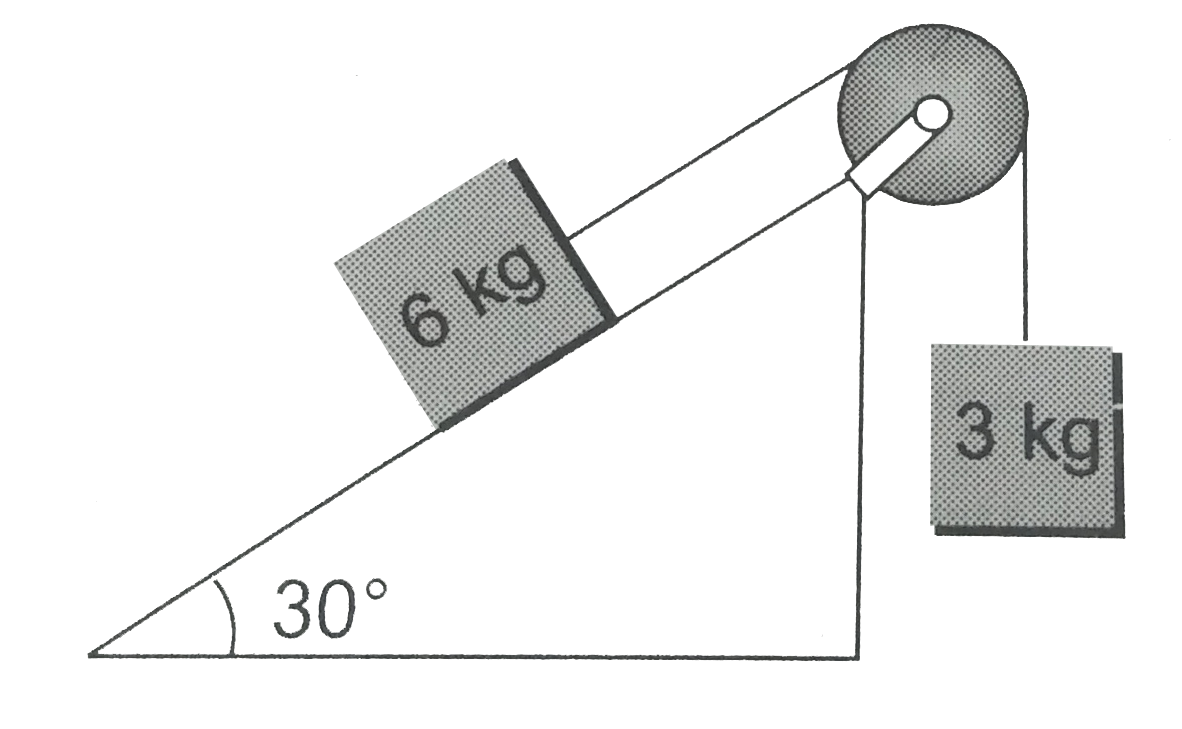 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2
Two bodies of mass 5 kg and 7 kg are suspended at the ends of massless string passing over frictionless pulley. The acceleration of the system.
View SolutionTwo masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is
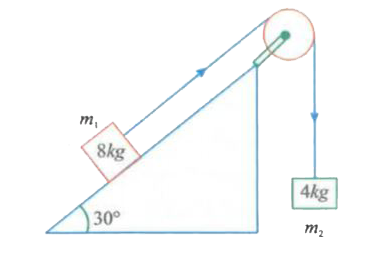 View Solution
View SolutionTwo masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is
 View Solution
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 View Solution
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View Solution

