Two blocks of masses M1 and M2 are connected by a string passing over a pulley as shown. The coefficient of friction between the block M1 and horizontal surface on which it lies is μ What additional mass m should be placed on M1 so that the system does not accelerate ?

(M2−M1)μ
M2−M1μ
M2μ−M1
M2−M1μ
The correct Answer is:c
There will be no acceleration if the driving force M2 g is equal to the total force of friction offered by (M1+m) i.e.
M2g=μ(M1+m)gorM2μ−M1=m
(c) is the choice.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-II)
64 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-III)
2 Videos
- HEAT AND THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - Recent Competitve Questions
17 Videos
- MAGNETOSTATICSBOOK - MODERN PUBLICATIONCHAPTER - MAGNETOSTATICSEXERCISE - RECENT COMPETITIVE QUESTION
5 Videos
Similar Questions
Two block of masses M1andM2 are connected with a string passing over a pulley as shown in figure The block M1 lies on a horizontal surface friction between the block M1 and the horizontal surface is μ The system accelerates. What additional mass m should be plased on the block M1 so that the system does not accelerate ?
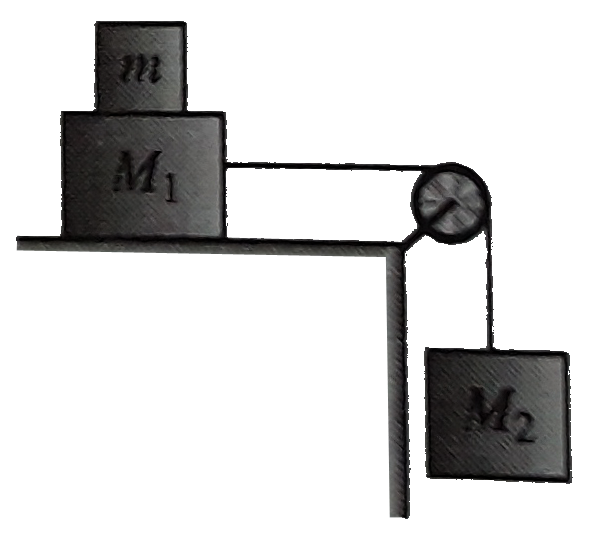
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View Solution
Knowledge Check
Two block of masses M1andM2 are connected with a string passing over a pulley as shown in figure The block M1 lies on a horizontal surface friction between the block M1 and the horizontal surface is μ The system accelerates. What additional mass m should be plased on the block M1 so that the system does not accelerate ?
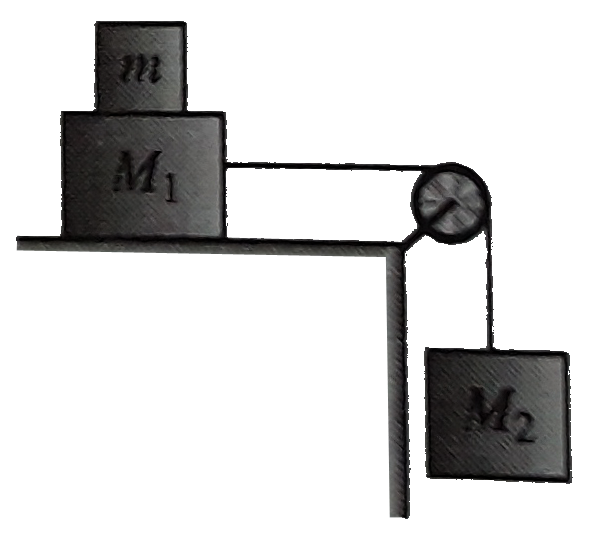 AM2−M1μBM2μ−M1CM2−M1μD(M2−M1)μ
AM2−M1μBM2μ−M1CM2−M1μD(M2−M1)μTwo blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgA large cubical shaped block of mass M rests on a fixed horizontal surface. Two blocks of mass m1 and m2 are connected by a light inextensible string passing over a light pulley as shown. Neglect friction everywhere. Then the constant horizontal force of magnitude F that should be applied to M so that m1 and m2 do not mov relative toM is:
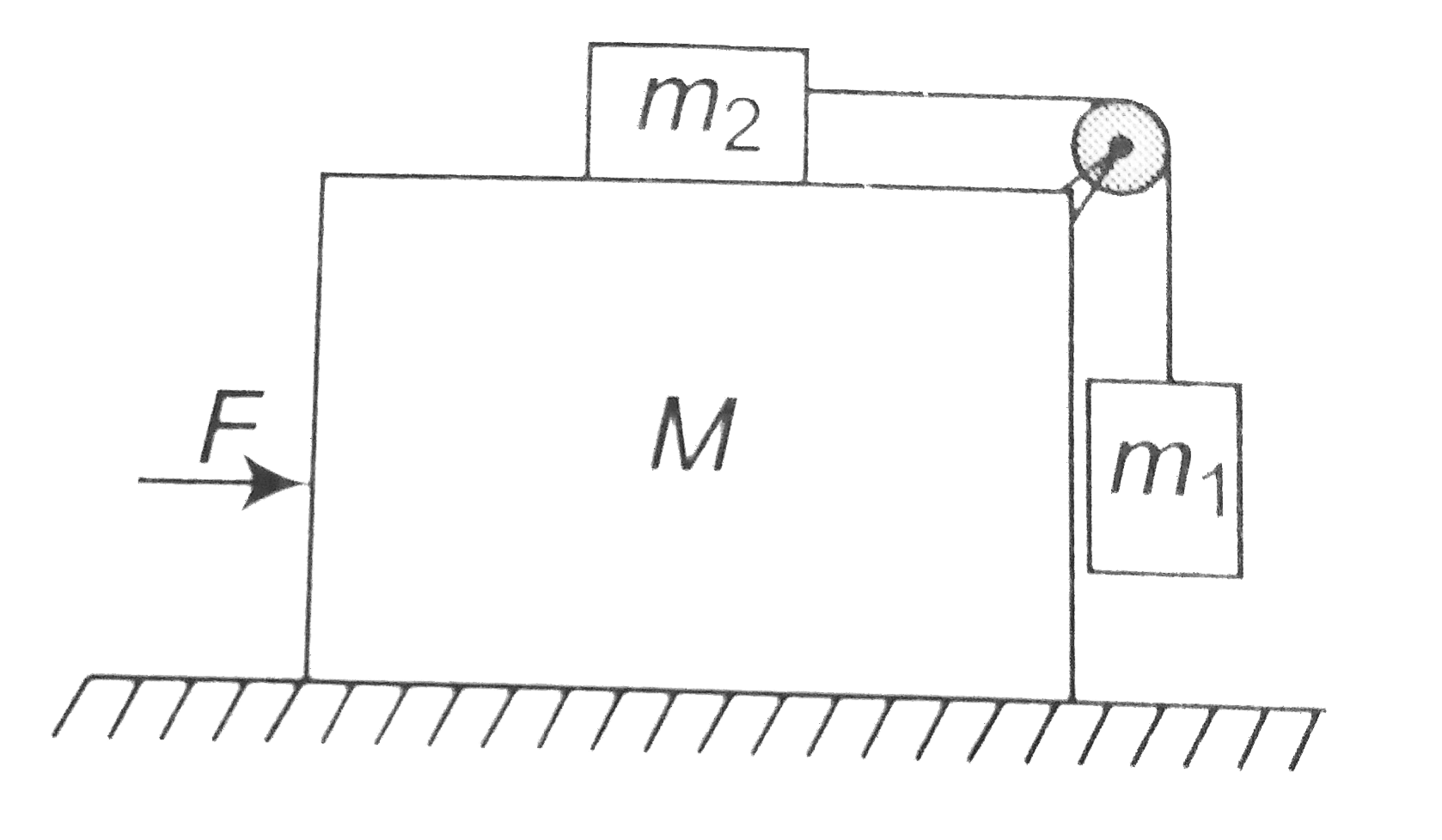 AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)g
AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)g
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution
