Two bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle α with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t.
The correct Answer is:[v0t√2(1−sinθ0)]
Step by step video, text & image solution for Two bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle alpha with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Advance MCQs with One or More Options Correct
17 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
Two bodies were thrown simultaneously from the same point , on straight up and the other, at angle θ=60∘ to the horizontal . The initial velocity of each body is equal to u=30m/s. Neglecting the air resistance, find the distance between the bodies after 2 seconds.
View SolutionTwo bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of θ=60∘ to the horizontal. The initial velocity of each body is equal to v0=25m/s. Neglecting the air drag, find the distance between the bodies t=1.70s later.
View Solution
Knowledge Check
Two bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
A2v0t+12>2B2v0tCv0t+12g t2Dv0tTwo bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
A1 : 1Bsinθ:cosθCsin2θ:cos2θDcosθ:sinθTwo projectiles are thrown from the same point simultaneously with same velocity 10ms−1. One goes straight vertically while other at 60∘ with the vertical . What will be the distance of separation between the after 1 second of their throw?
A20mB10mC5mD15m
Two bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance (in meter) between the bodies at t=1.2 later is
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneously towards each other, one is thrown horizontally with a velocity of 8m/s and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. This horizontal distance between points A and B equal to 8m.Then find
a)The initial velocity V0 of the body thrown at an angle 45∘
b)The time of flight t of the bodies before colliding
c) The coordinate (x,y) of the point of collision (consider the bottom of the tower A as origin )is
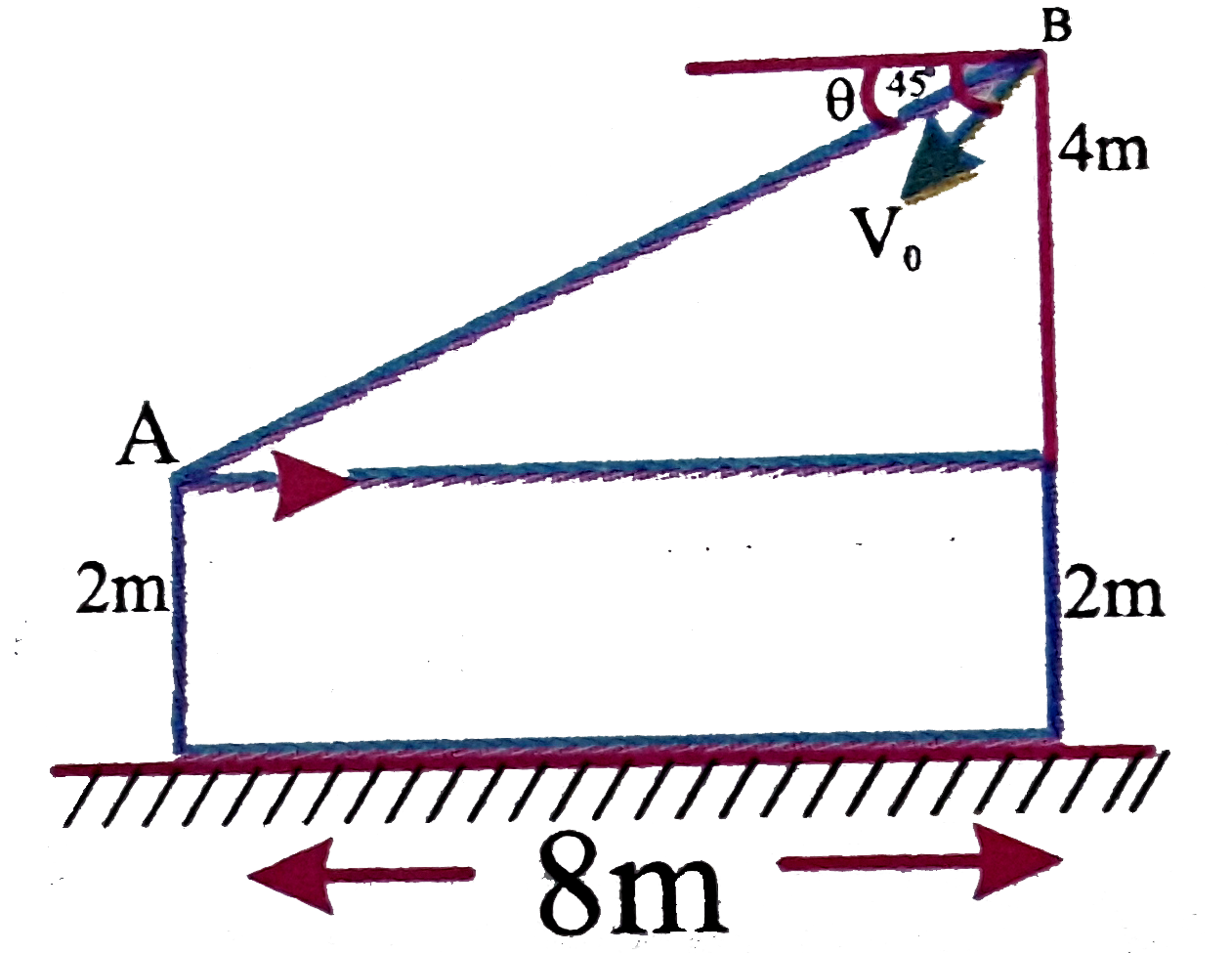
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of 8ms and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity V0 of the body thrown at an angle 45∘
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) is
View SolutionTwo bodies are thrown with the same velocity at angles α and 90∘−α to the horizontal.Calculate the ratio of the maximum heights reached by the bodies.
View SolutionA body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View Solution
