Two cars C1 and C2 moving in the same direction on a straight single lane road with velocities v1=12ms−1 and v2=10ms−1, respectively . When the separation between the two was d=200m, C2 started accelerating to avoid collision. What is the minimum acceleration of car C2 so that they do not collide?
 .
.
Acceleration is just avoided if the relative velocity becomes zero just at the moment the two cars meet each other, i.e.
→a2=→a1−→ac1−→ac_(2)=0−a(−a)
→u12=→u1−→u2=12−10=2ms−2
The collsion is just avoided if the relative velocity becomes zero just at the moment the two cars meer each other, i.e.,
v12=0 when s12=200.
Now v12=0,→u12=2,=→a12=−a, and s12=200.
v212−u212=2a12s12becuase0−22=−2×a×200
→a−1100ms−2=0.1ms−2=1cms−2
Therefore, minimum acceleration needed by car c2=1cms−2.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Subjective
29 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.2
12 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
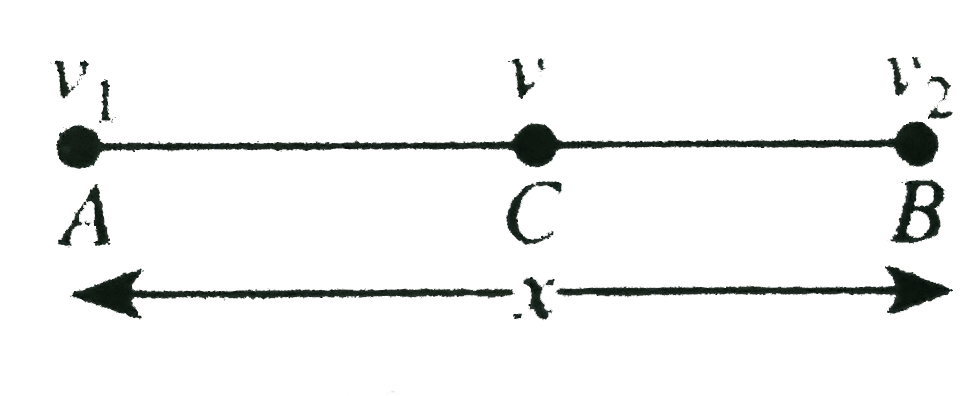 .
.
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View Solution
Knowledge Check
Two cars C1 and C2 are moving on parallel roads in the same direction with velocity v. The relative of C1 w.r.t. C2 is :
ADirection towards C2BDirection towards C1CZeroD2vTwo bodies starts moving from same point along straight line with velocities v1=6m/s and v2=10m/s
simultaneously. After what time the separation becomes 40 m ?A6 sB8 sC12 sD10 sTwo particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then
 Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m
Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m
Car A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
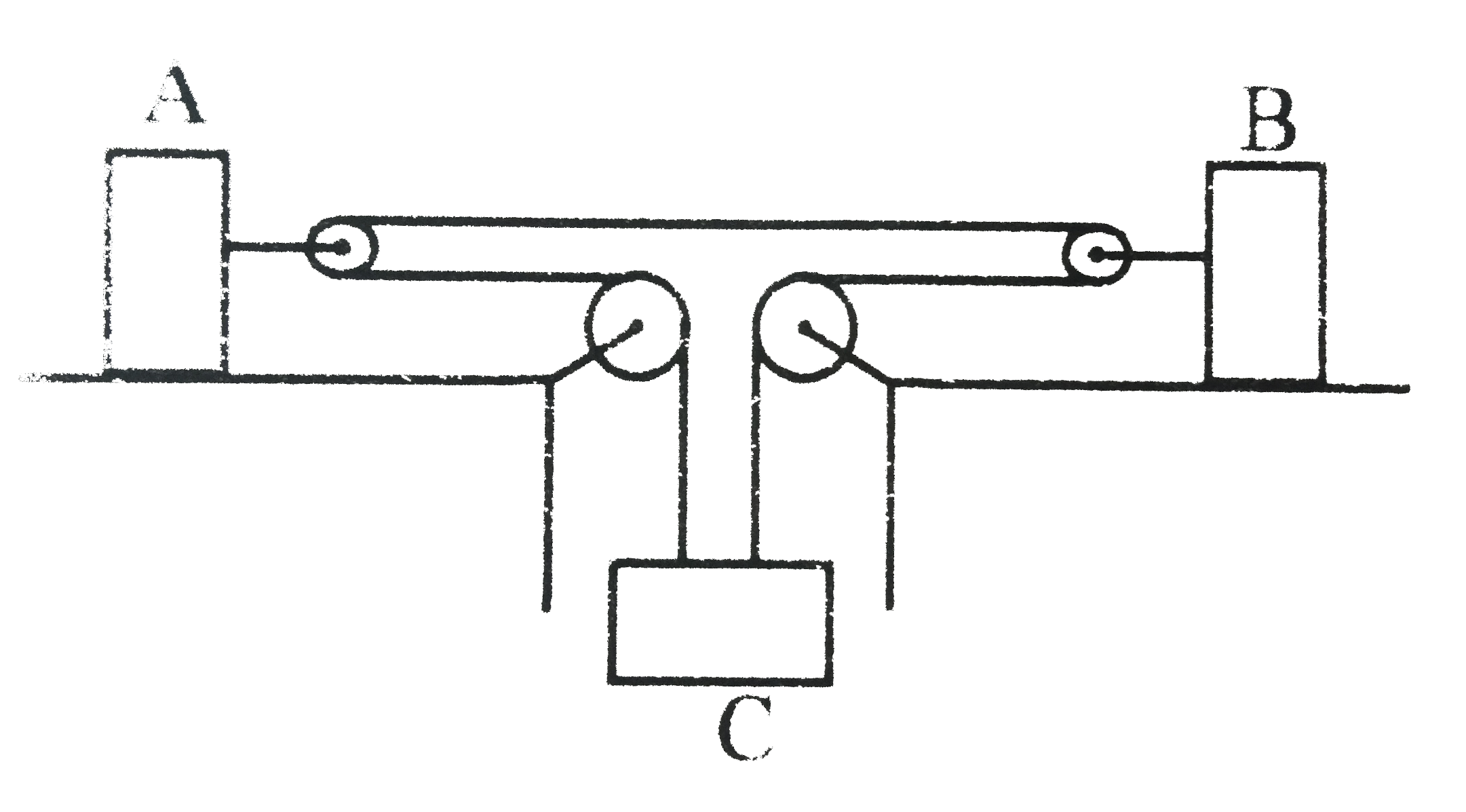
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionTwo particles of mass m and 2 m moving in opposite directions collide elastically with velocities v and 2v. Find their velocities after collision.
View Solution
