Two charged particle A and B repel each other by a force kr2 where is a constant and r is th separation between them. The particle A is clamped to a fixed point in the lab and the particle B which has a mass m, is released from rest with asn initial separartion r0 form A. Find the change in the potential energyof hte wo particle system as the separation increases to a large value. What will be the speed o the particle b in this situation?

The situation is shown in ure. Take A+B as the system. The only exterN/Al force acting on the system is that needed to hold A fixed. (you can imagine the experimetn being conducted in a gravity freee region or the particles may be kept and allowed to move on a smooth horizontal surface, so that teh normal force balaces the force of gravity). This force does no work on the system because it acts on teh charge A which does not move. Thus, the exterN/Al forces do no work and internl forces ae conservative. The total mechanical energy must, therefore, remain constant. There are two interN/Alforces FAB acting on A andFBA acting on B. The force FAB does no work beause it acts on A which does not moe. The work done by FBA as the particle B is taken away is,
W=∫→F.→dr=∫∞_r0kr2dr=kr0............i

The change in the potential energy of the system is Uf−Ui=−W=−kr0
As the total mechanical energy of the system is
Kf+Uf=Ki+Ui
or Kf=Ki−(Uf−Ui)
or, 12mv2=kr0
or,v=√2kmr0
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Worked out Examples
14 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -1
10 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
Two point charges separated by a distance d repel each other with a force of 9N. If the separation between them becomes 3d, the force of repulsion will be
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution
Knowledge Check
A particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle A. Treat the collision as elastic.
Ah2mAv[(mA+mB)(mA−mB)−1]BhmAv[(mA−mB)(mA+mB)−1]ChmAv[(mA+mB)(mA−mB)−1]D2hmAv[(mA+mB)(mA−mB)+1]
A particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de-Broglie wavelength of the particle A. Treat the collision as elastic.
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of +4.0×10−5C. They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
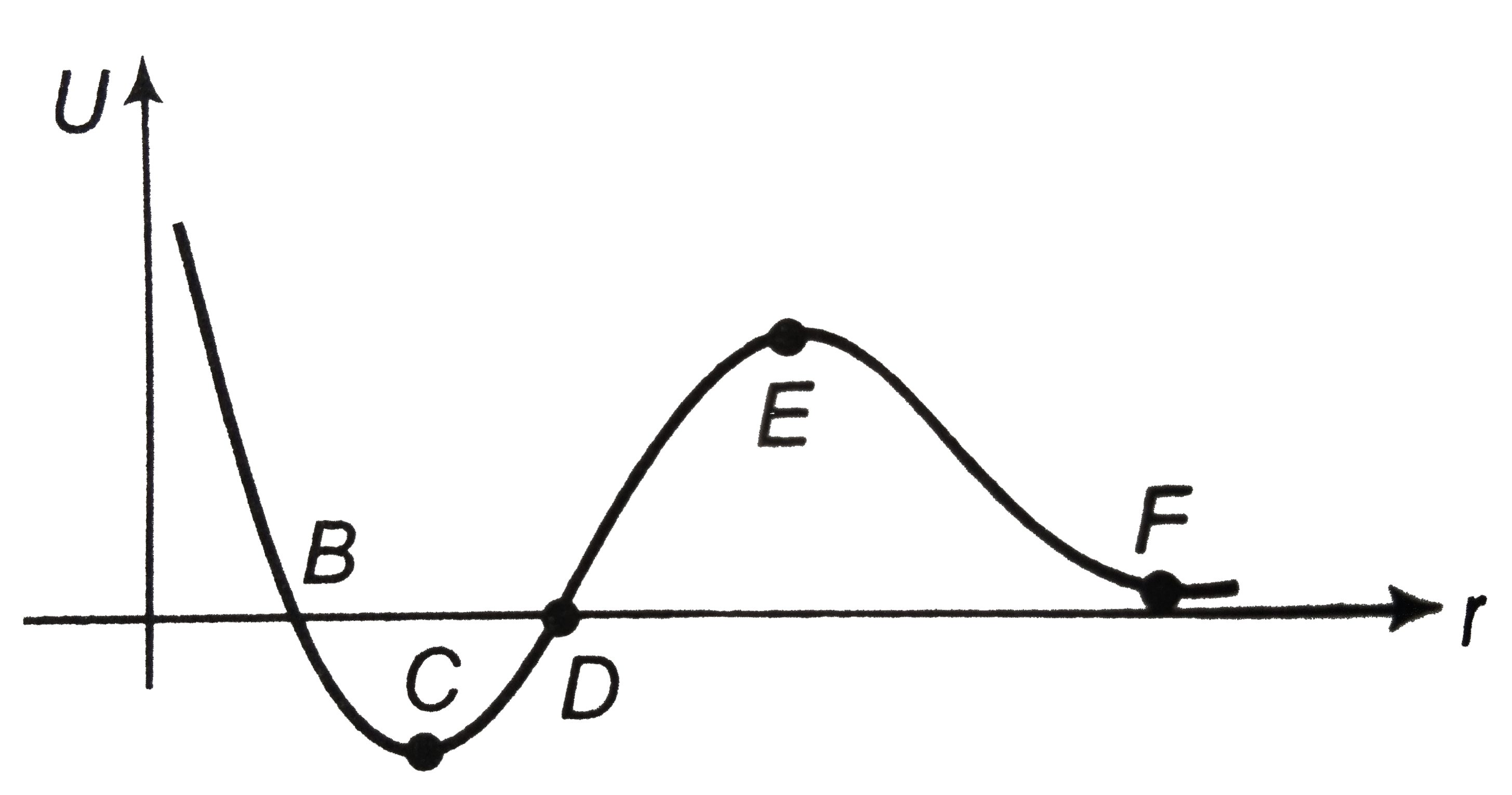
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View SolutionTwo charged particles having charges 1and−1μC and of mass 50g each are held at rest while their separation is 2m. Now the charges are released. Find the speed of the particles when their separation is 1m.
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
View Solution
