A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
Eq2m2t2
2E2t2mq
E2q2t22m
Eqm2t
The correct Answer is:C
To find the kinetic energy of a charged particle of mass m and charge q released from rest in a constant electric field E after a time t, we can follow these steps:
Step 1: Understand the Force Acting on the Particle
The force F acting on the charged particle due to the electric field is given by:
\( F = qE \)
where q is the charge of the particle and E is the magnitude of the electric field.
Step 2: Calculate the Acceleration of the Particle
Using Newton's second law, the acceleration a of the particle can be calculated as:
\( a = \frac{F}{m} = \frac{qE}{m} \)
where m is the mass of the particle.
Step 3: Determine the Velocity After Time t
Since the particle is released from rest, its initial velocity v0 is 0. The final velocity v after time t can be calculated using the equation of motion:
\( v = v_0 + at \)
Substituting the values, we get:
\( v = 0 + \left(\frac{qE}{m}\right)t = \frac{qEt}{m} \)
Step 4: Calculate the Kinetic Energy
The kinetic energy (KE) of the particle after time t is given by the formula:
\( KE = \frac{1}{2} mv^2 \)
Substituting the expression for v from Step 3:
\( KE = \frac{1}{2} m \left(\frac{qEt}{m}\right)^2 \)
Simplifying this expression:
\( KE = \frac{1}{2} m \cdot \frac{q^2 E^2 t^2}{m^2} = \frac{q^2 E^2 t^2}{2m} \)
Final Answer
Thus, the kinetic energy of the particle after time t is:
\( KE = \frac{q^2 E^2 t^2}{2m} \)
---
The force F acting on the charged particle due to the electric field is given by:
\( F = qE \)
where q is the charge of the particle and E is the magnitude of the electric field.
Using Newton's second law, the acceleration a of the particle can be calculated as:
\( a = \frac{F}{m} = \frac{qE}{m} \)
where m is the mass of the particle.
Since the particle is released from rest, its initial velocity v0 is 0. The final velocity v after time t can be calculated using the equation of motion:
\( v = v_0 + at \)
Substituting the values, we get:
\( v = 0 + \left(\frac{qE}{m}\right)t = \frac{qEt}{m} \)
The kinetic energy (KE) of the particle after time t is given by the formula:
\( KE = \frac{1}{2} mv^2 \)
Substituting the expression for v from Step 3:
\( KE = \frac{1}{2} m \left(\frac{qEt}{m}\right)^2 \)
Simplifying this expression:
\( KE = \frac{1}{2} m \cdot \frac{q^2 E^2 t^2}{m^2} = \frac{q^2 E^2 t^2}{2m} \)
Thus, the kinetic energy of the particle after time t is:
\( KE = \frac{q^2 E^2 t^2}{2m} \)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
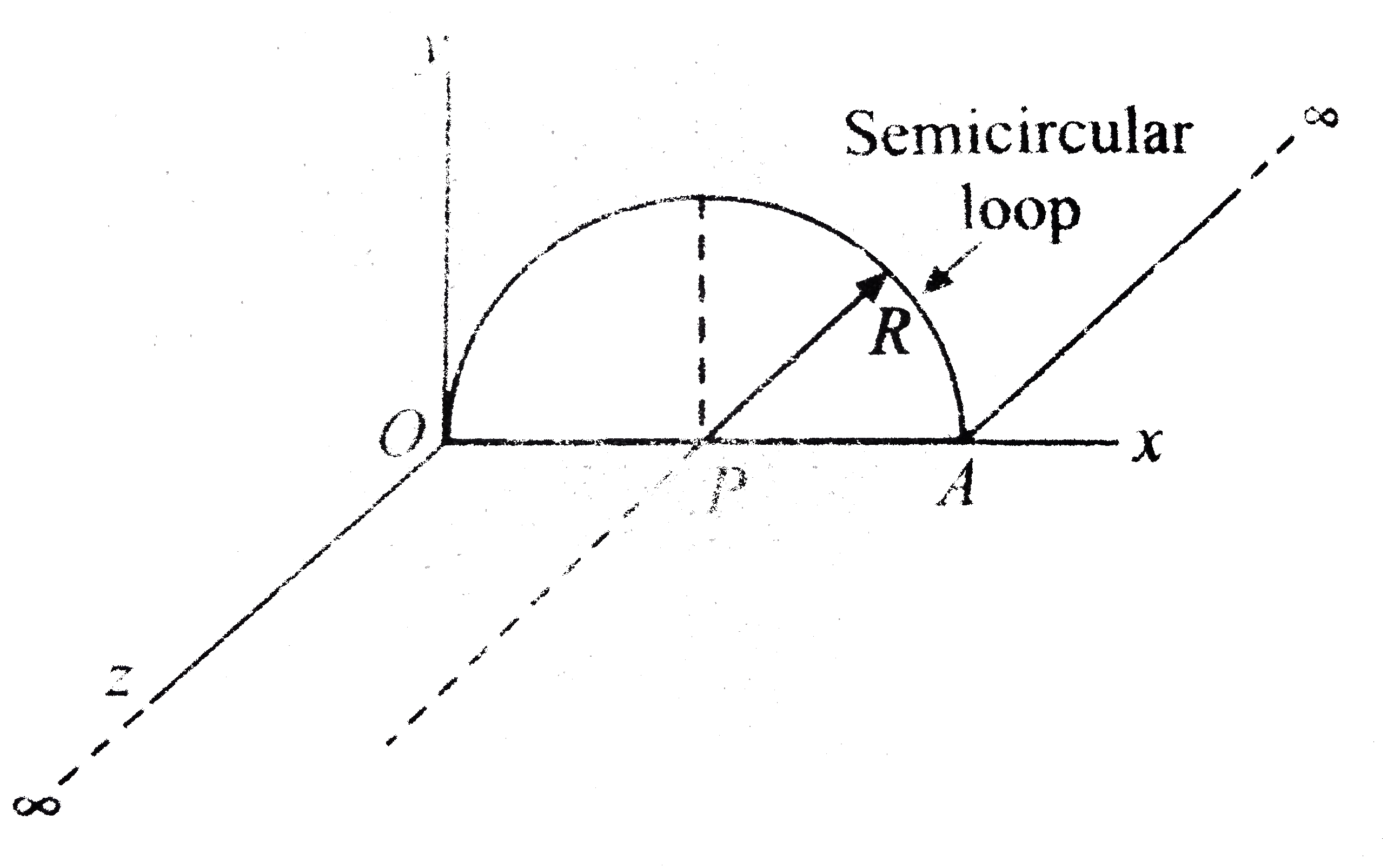
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View SolutionA particle of mass ma and charge q is released from rest in a uniform filed of magnitude E. the uniform field is created between two parallel plates of charge densities +σ and −σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it stirkes the opposite plate.

View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View Solution
