Two circular loops of radius r and R ( $R > > r$ ) are placed coaxially with their centres coinciding. What will be the mutual inductance for the pair? If one of the coils is rotated through $90^{\circ}$ angle, then what will be the new mutual inductance?

Video Solution

Text Solution

Verified by Experts

Let the bigger coil be primary, then magnetic field near its centre is given by the following relation:
$B = \frac{μ_{0} i}{2 R}$
This magnetic field may be assumed as constant for the small coil. Moreover, direction of magnetic field is perpendicular to the plane of smaller coil and hence flux associated can be calculated by just multiplying field intensity with area as follows:
$ϕ = (\frac{μ_{0} i}{2 R}) \times (π r^{2})$
On comparing above equation with $ϕ = M i$ we get mutual inductance of the pair as follows:
$ϕ = (\frac{μ_{0} i}{2 R}) \times (π r^{2}) = M i$
$\Rightarrow M = \frac{μ_{0} π r^{2}}{2 R}$
When the smaller coil is rotated by $90^{\circ}$ angle then magnetic field becomes parallel to its plane and hence flux becomes zero and hence mutual inductance becomes zero.

Updated on:21/07/2023

Two concentric co - planar circular loops of radius R and $r (< < R)$ are placed as shown in the figure. The mutual inductance of the system will be

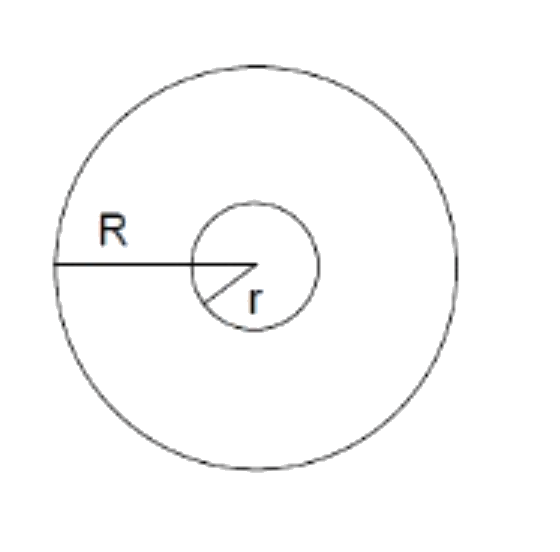A $\frac{π μ_{0} r^{2}}{2 R}$
B $\frac{π μ_{0} r^{2}}{4 R}$
C $\frac{π μ_{0} R^{2}}{4 r}$
D $\frac{π μ_{0} R^{2}}{2 r}$
Two concentric circular coils, one of small radius $r_{1}$ and the other of large radius $r_{2}$ such that $r_{1} < < r_{2}$ are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
A $\frac{μ_{0} π t r_{1}^{2}}{2 r_{2}}$
B $\frac{μ_{0} π t r_{2}^{2}}{2 r_{1}}$
C $\frac{μ_{0} π t r_{2}^{2}}{r_{1}}$
D $\frac{μ_{0} π t r_{1}^{2}}{r_{2}}$