Two circular coils, one of smaller radius $r_{1}$ and the other of very large radius $r_{2}$ are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.

Video Solution

Text Solution

Verified by Experts

Suppose a current $I_{2}$ flows through the outer circular coil. The field at the centre of the coil is

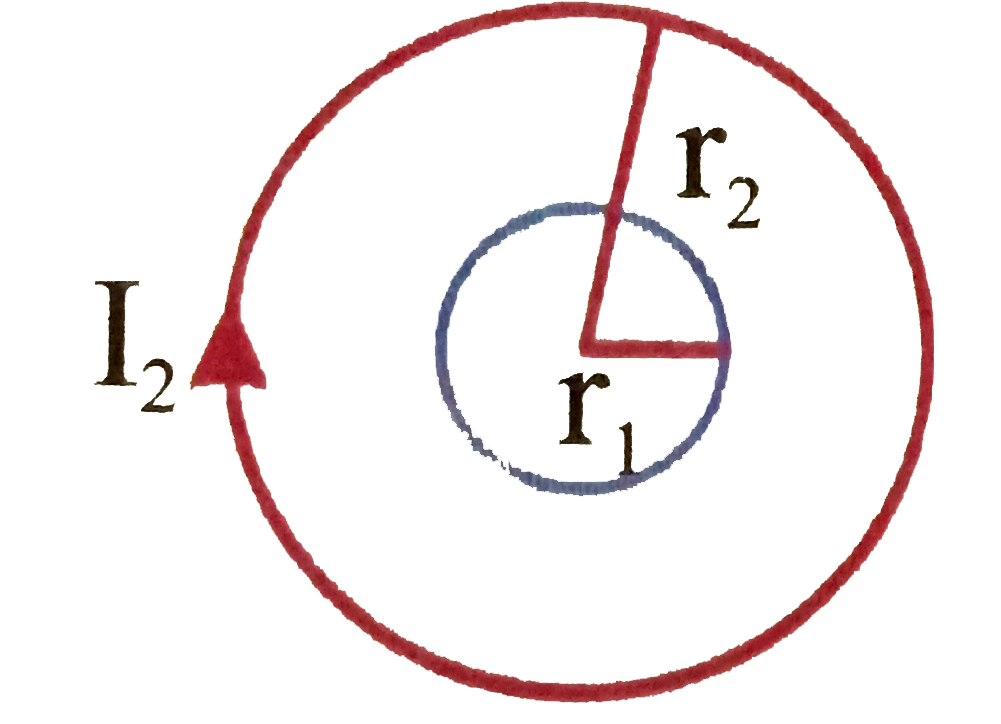
$B_{2} = \frac{μ_{0} I_{2}}{2 r_{2}}$
The second co-axially placed coil has very small radius. So $B_{2}$ may be considered constant over its cross-sectional area.
Now, $ϕ_{1} = π r_{1}^{2} B_{2} = π r_{1}^{2} (\frac{μ_{0} I_{2}}{2 r_{2}})$ or $ϕ_{1} = \frac{μ_{0} π r_{1}^{2}}{2 r_{2}} I_{2}$
Comparing with $ϕ_{1} = M_{12} I_{2}$ , we get , $M_{12} = \frac{μ_{0} π r_{1}^{2}}{2 r_{2}}$
Aslo, $M_{21} = M_{12} = \frac{μ_{0} π r_{1}^{2}}{2 r_{2}} \Rightarrow M \propto \frac{r_{1}^{2}}{r_{2}}$
It would have been difficult to calculate the flux through the bigger coil nouniform field due to the current in the smaller coil and hence the mutual inductance $M_{12}$ . The equality $M_{12} = M_{21}$ is helpful. Note also that mutual inductance depends solely on the geometry.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two concentric circular coils, one of small radius $r_{1}$ and the other of large radius $r_{2}$ such that $r_{1} < < r_{2}$ are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
A $\frac{μ_{0} π t r_{1}^{2}}{2 r_{2}}$
B $\frac{μ_{0} π t r_{2}^{2}}{2 r_{1}}$
C $\frac{μ_{0} π t r_{2}^{2}}{r_{1}}$
D $\frac{μ_{0} π t r_{1}^{2}}{r_{2}}$
Question 2 - Select One
Two coil are placed close to each other. The mutual inductance of the pair of coils depends upon.
Athe rates at which currents are changing in the two coils
Brelative position and orientation of hte two coils
Cthe materials of the wires of he coils
Dthe currents in the two coils
Question 3 - Select One
A long straight wire is placed along the axis of a circuit ring of radius R. The mutual inductance of this system is
A $\frac{μ_{0} R}{2}$
B $\frac{μ_{0} π R}{2}$
C $\frac{μ_{0}}{2}$
D $0$

NARAYNA-ELECTRO MAGNETIC INDUCTION-Level-II (H.W)

Home
Ask Doubt
Profile