Two concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

At P,F=0
At Q, F=GM1mb2
At R, F=G(M1)+(M2)mc2.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Knowledge Check
Consider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P isAG(M1+M2)y2,G(M1+M2)y2BG(M1+M2+M3)Y2,G(M1+M2)x2CG(M1+M2+M3)a2,GM1a2DG(M1+M2+M3)C2,GM2b2Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
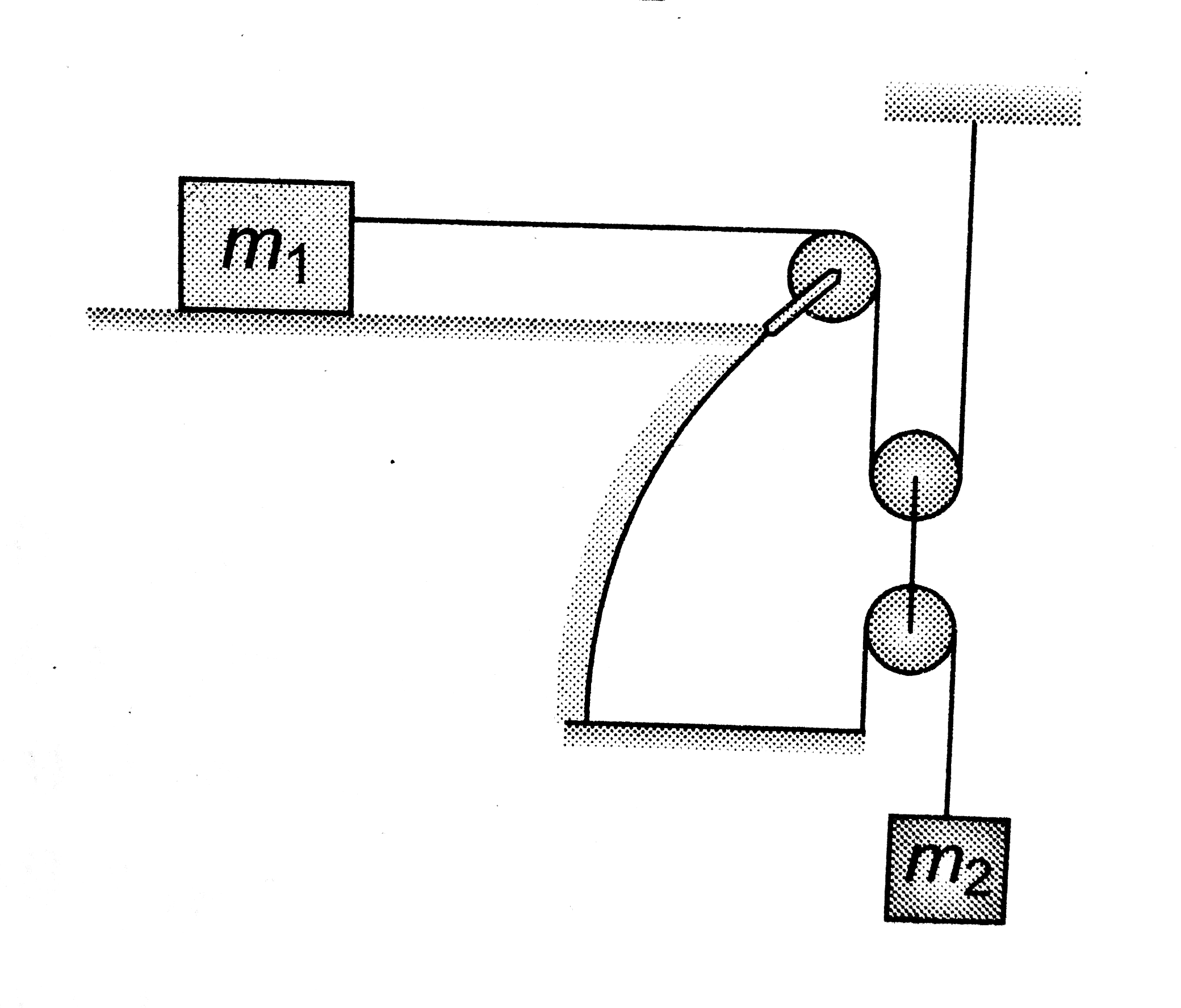 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
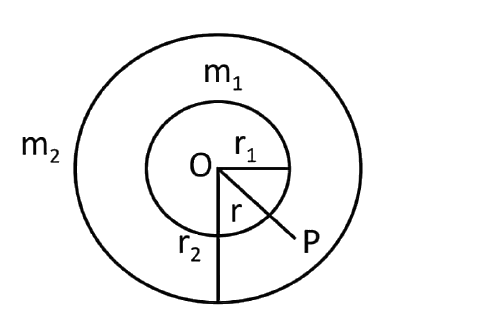
Two concentric shells of mass m1 and m2 are situated as shown. Find the force on a particle of mass m when the particles is located at (a)r=r1,(b)r=r2,(c)r=r3. The distance r is measured from the centre of the shell.

View SolutionTwo concentric shells of different mass m1 and m2 are having a sliding particle of mass m. The forces on the sliding at positions I,II and III are respectively

View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View Solution