Two conducting plates A and B are placed parallel to each other. A is given a charge. and B a charge . Find the distribution of charges on the four surface.
To solve the problem of charge distribution on the four surfaces of two parallel conducting plates A and B, we will follow these steps:
Step 1: Identify the Plates and Charges
- Let plate A have charge Q1 and plate B have charge Q2.
- Each plate has two surfaces: an inner surface (facing each other) and an outer surface (facing away from each other).
Step 2: Define the Surfaces
- For plate A:
- Inner surface: Q2
- Outer surface: Q4
- For plate B:
- Inner surface: Q3
- Outer surface: Q1
Step 3: Apply Gauss's Law
- According to Gauss's Law, the electric field inside a conductor in electrostatic equilibrium is zero. This implies that the net charge on the inner surfaces of the plates must balance each other.
Step 4: Charge Distribution on the Surfaces
1. Outer Surface of Plate A (Q4):
- The outer surface of plate A will have a charge equal to the total charge on plate A, which is Q1.
- Thus, Q4=Q1.
2. Inner Surface of Plate A (Q2):
- The inner surface of plate A must have a charge that balances the electric field due to charge Q2 on plate B.
- Therefore, the charge on the inner surface of plate A is:
Q2=Q1−Q1+Q22
- Simplifying this gives:
Q2=Q1−Q22
3. Inner Surface of Plate B (Q3):
- The inner surface of plate B must also balance the electric field due to charge Q1 on plate A.
- Therefore, the charge on the inner surface of plate B is:
Q3=−(Q1−Q1+Q22)
- Simplifying this gives:
Q3=Q2−Q12
4. Outer Surface of Plate B (Q1):
- The outer surface of plate B will have a charge equal to the total charge on plate B, which is Q2.
- Thus, Q1=Q2.
Summary of Charge Distribution
- Outer surface of plate A: Q4=Q1
- Inner surface of plate A: Q2=Q1−Q22
- Inner surface of plate B: Q3=Q2−Q12
- Outer surface of plate B: Q1=Q2
Final Charge Distribution
- Q4=Q1
- Q2=Q1−Q22
- Q3=Q2−Q12
- Q1=Q2
- Let plate A have charge Q1 and plate B have charge Q2.
- Each plate has two surfaces: an inner surface (facing each other) and an outer surface (facing away from each other).
- For plate A:
- Inner surface: Q2
- Outer surface: Q4
- For plate B:
- Inner surface: Q3
- Outer surface: Q1
- According to Gauss's Law, the electric field inside a conductor in electrostatic equilibrium is zero. This implies that the net charge on the inner surfaces of the plates must balance each other.
1. Outer Surface of Plate A (Q4):
- The outer surface of plate A will have a charge equal to the total charge on plate A, which is Q1.
- Thus, Q4=Q1.
- The inner surface of plate A must have a charge that balances the electric field due to charge Q2 on plate B.
- Therefore, the charge on the inner surface of plate A is:
Q2=Q1−Q1+Q22
- Simplifying this gives:
Q2=Q1−Q22
- The inner surface of plate B must also balance the electric field due to charge Q1 on plate A.
- Therefore, the charge on the inner surface of plate B is:
Q3=−(Q1−Q1+Q22)
- Simplifying this gives:
Q3=Q2−Q12
- The outer surface of plate B will have a charge equal to the total charge on plate B, which is Q2.
- Thus, Q1=Q2.
- Outer surface of plate A: Q4=Q1
- Inner surface of plate A: Q2=Q1−Q22
- Inner surface of plate B: Q3=Q2−Q12
- Outer surface of plate B: Q1=Q2
- Q4=Q1
- Q2=Q1−Q22
- Q3=Q2−Q12
- Q1=Q2
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 1
6 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 2
8 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
Two conducting plates A and B are placed parallel to each other. A is given a charge Q1 and B a charge Q2. Prove that the charges on the inner surfaces are of equal magnitude and opposite sign.
View SolutionTwo nonconducting infinite planes sheets having charges Q and 2Q are placed parallel to each other as shown in figure. The charge distribution on the four faces of the two plates is also shown. The electric field intensities at three points 1, 2, and 3 are →E1,→E2,and→E3, respectively. Then the magnitudes of →E1,→E2,and→E3 are, respectively (surface area of plates ) :

View Solution
Knowledge Check
Two large parallel conducting plates are placed close to each other ,the inner surface of the two plates have surface charge densities +σ and −σ .The outer surfaces are without charge.The electric field has a magnitude of
A(sigma)/(epsi_(0)) in the region between the platesB''σε0 in the region between the platesC0Dnone of these
Two large conducting plates are placed parallel to each other with a separation of 2.00 cm betweeen them. An electron starting from rest near one of the plates reaches the other plate in 2.00 microseconds. Find the surface charge density on the inner surfaces.
View SolutionX and Y are large, parallel conducting plates close to each other. Each face has an area A. X is given a charge Q. Y is without any charge. Points A,B and C are as shown in the figure.

View SolutionTwo conducting plates X and Y, each having large surface aera A (on one side), are placed parallel to each other as show in figure.

Find the surface charge density at the inner surface of the plate X.
View SolutionThree large conducting sheets placed parallel to each other at a finite distance contain charges Q,−2Q,and3Q, respectively. Find the electric fields at points A, B, C, and D.
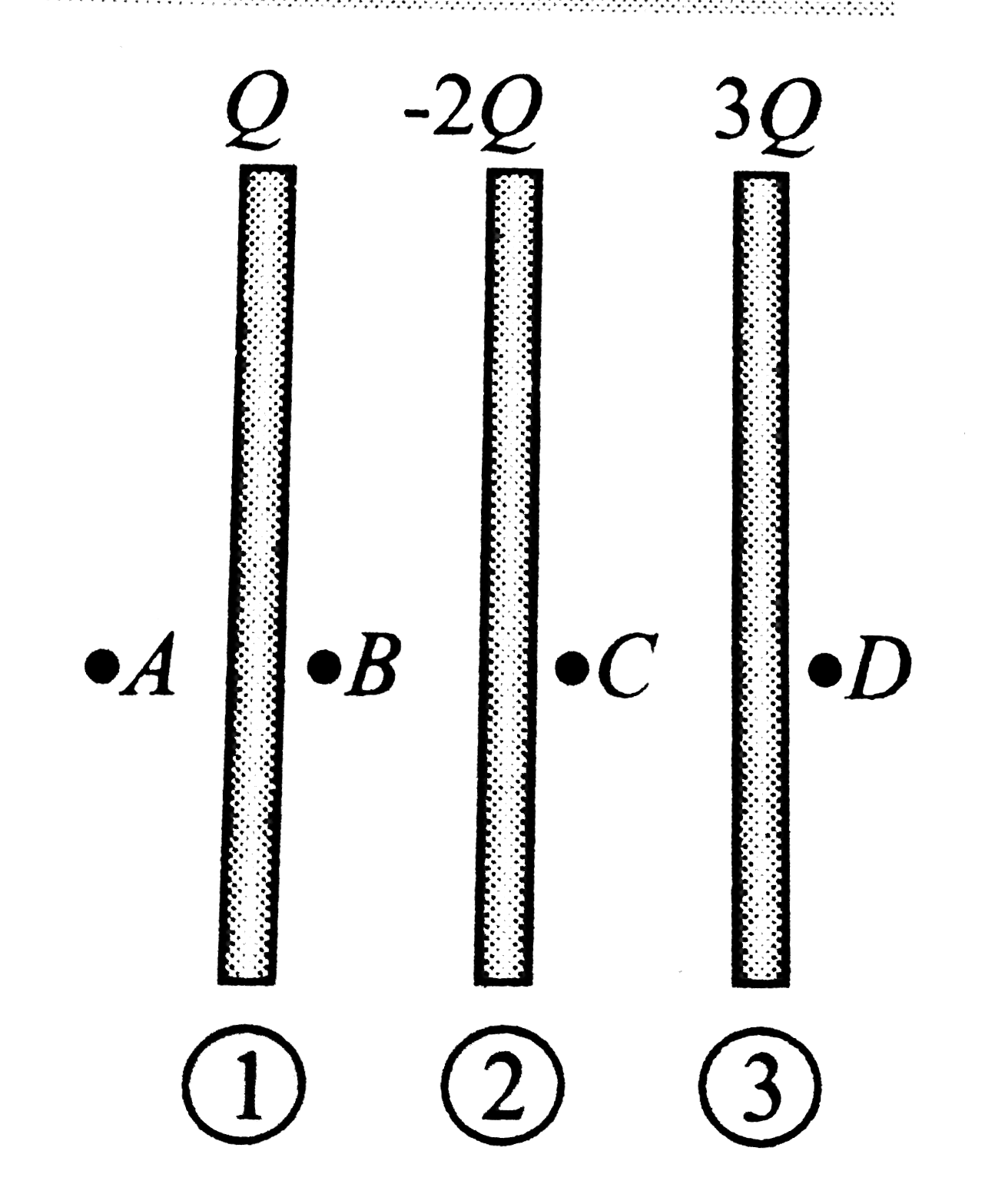
View SolutionThe nagative plate of a parallel plate capacitor is given a charge of −20X10−8C. Find the charges appearing on the four surface of the capacitor plates.
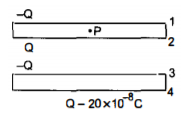
View SolutionTwo conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then

View SolutionThree parallel metalic plates each of area A are kept as shown in figure and charges q1,q2 and q3 are given to them. Find the resulting charge distribution on the six surfaces, neglecting edge effects as usual,

View Solution
