A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10Vm−1. If the plastic plate is replaced by a copper plate of the same geometrical dimension and carrying the same charge Q the electric field at the point P will become
zero
5Vm−1
10Vm−1
20Vm−1.
The correct Answer is:C
To solve the problem, we need to analyze the electric field produced by both the plastic and copper plates when they carry the same charge Q.
Step 1: Understand the Electric Field from the Plastic Plate
The electric field E at point P close to the center of a large non-conducting plate with uniform charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Given that the electric field at point P is 10V/m, we can write:
σ2ϵ0=10
From this, we can express the surface charge density σ:
σ=20ϵ0
Step 2: Analyze the Copper Plate
When the plastic plate is replaced by a copper plate (which is a conductor), the charge Q will redistribute itself on the surface of the conductor. For a conductor, the electric field inside the conductor is zero, and the charge resides on the outer surface.
The surface charge density on the outer surface of the copper plate is:
σ′=QA
where A is the area of the plate.
Step 3: Calculate the Electric Field from the Copper Plate
For a conducting plate, the electric field outside the plate (at point P) is given by:
E′=σ′ϵ0
Since the charge Q is uniformly distributed, the surface charge density σ′ can be expressed as:
σ′=QA
Thus, the electric field at point P becomes:
E′=Q/Aϵ0
Step 4: Relate the Electric Fields
From the previous steps, we have:
1. For the plastic plate: E=σ2ϵ0=10V/m
2. For the copper plate: E′=Q/Aϵ0
Now, we know that:
σ=20ϵ0
Thus, substituting σ into the equation for the electric field of the copper plate, we can find:
E′=Q/Aϵ0=2⋅σ2ϵ0=2⋅10=20V/m
Final Answer
The electric field at point P when the plastic plate is replaced by a copper plate will be:
20V/m
The electric field E at point P close to the center of a large non-conducting plate with uniform charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
σ2ϵ0=10
From this, we can express the surface charge density σ:
σ=20ϵ0
When the plastic plate is replaced by a copper plate (which is a conductor), the charge Q will redistribute itself on the surface of the conductor. For a conductor, the electric field inside the conductor is zero, and the charge resides on the outer surface.
σ′=QA
where A is the area of the plate.
For a conducting plate, the electric field outside the plate (at point P) is given by:
E′=σ′ϵ0
Since the charge Q is uniformly distributed, the surface charge density σ′ can be expressed as:
σ′=QA
E′=Q/Aϵ0
From the previous steps, we have:
1. For the plastic plate: E=σ2ϵ0=10V/m
2. For the copper plate: E′=Q/Aϵ0
σ=20ϵ0
Thus, substituting σ into the equation for the electric field of the copper plate, we can find:
E′=Q/Aϵ0=2⋅σ2ϵ0=2⋅10=20V/m
The electric field at point P when the plastic plate is replaced by a copper plate will be:
20V/m
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 2
8 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Exercises
24 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Work Out Exaples
8 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
Charge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionTwo large conducting plates X and Y. each having large surface area A (on one side), are placed parallel to each other as shown in figure (30-E7). The plate X is given a charge Q whereas the other is neutral. Find (a) the surface charge density at the inner surface of the plates X, (b) the electric field at a point to the left of the plates, (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.

View SolutionA parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionTwo point charges q AND 2q are placed at (a,0) and (0,a) A point charge q1 is placed at a P on the quarter circle of radius a as shown in the diagram so that the electric field at the origin becomes zero
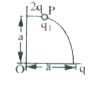
View SolutionAn uncharged parallel plate capacitor is connected to a battery. The electric field between the plates is 10V/m. Now a dielectric of dielectric constant 2 is inserted between the plates filling the entries space. The electric field between the plates now is
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionA point charge q is situated at X between two parallel plates which have a potential difference V and carry charges +Q and −Q. What is the electric field strength at X ?

View Solution
