Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
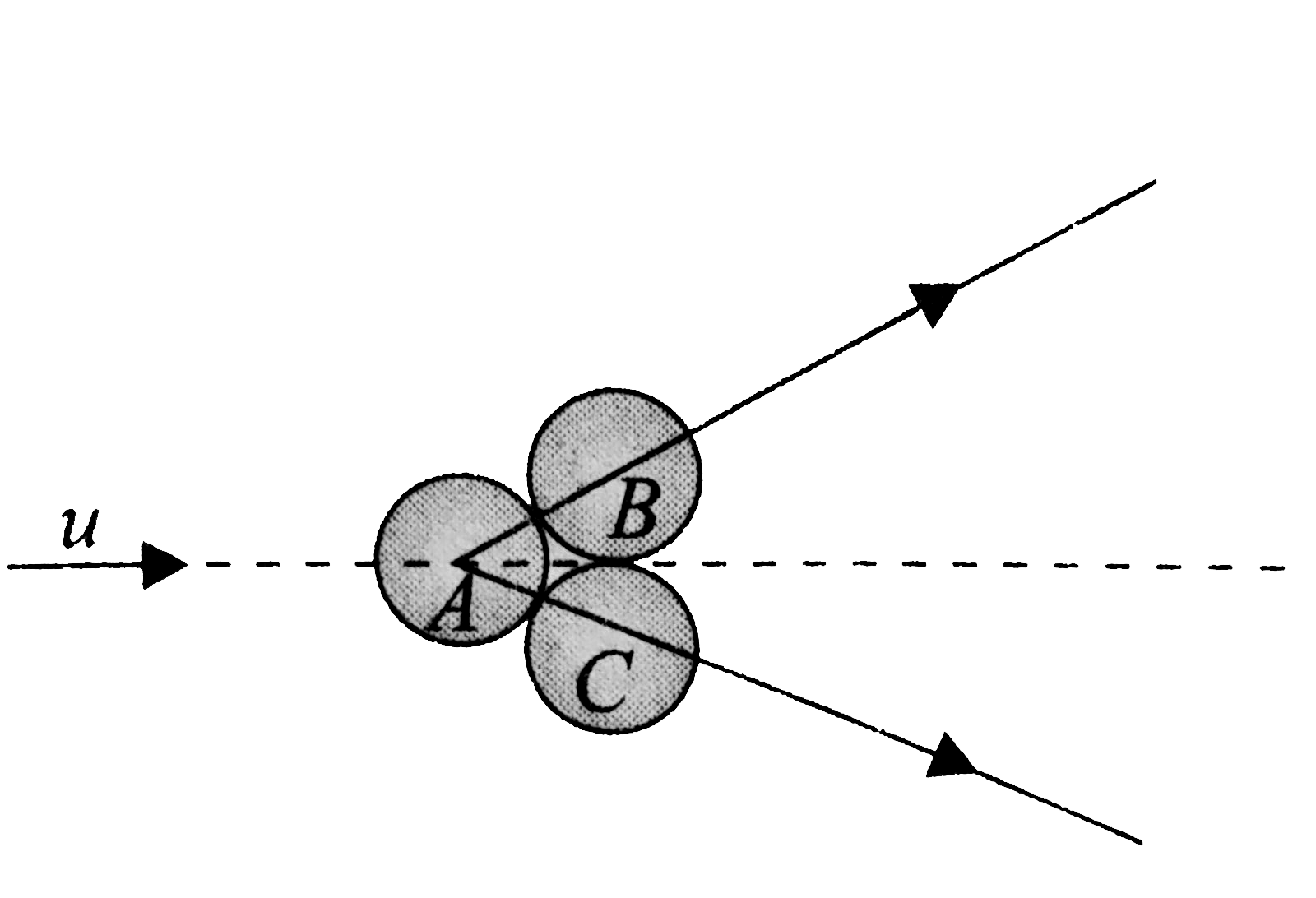
Find the velocity acquired by each of the spheres B and C after collision.
u√3
2u√3
u2√3
u2
The correct Answer is:C
u=velocity of sphere A before impact. As the spheres are identical, the triangle ABC formed by joining their centres is equilateral. The spheres B and C will move in direction AB and AC after impact making can angle of 30∘ with the origina lines of motion of ball A.
Let v be the speed ofthe balls B and C after impact.
Momentum conservation gives
(m2)u=mvcos30∘+mvcos30∘
u=2√3v⇒v=u2√3.......i
From Newton's experimental law, for an oblique collision, we have take components along normal, i.e. along AB for balls A and B.
vB−vA=−e(uB−uA)
v−0=−e(0−ucos30∘)
v=eucos30∘.........ii
Combining eqn i and ii we get e=13
Loss in KE=12m2u2−2(12mv2)
=14μ2−m(u2√3)2=16μ2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
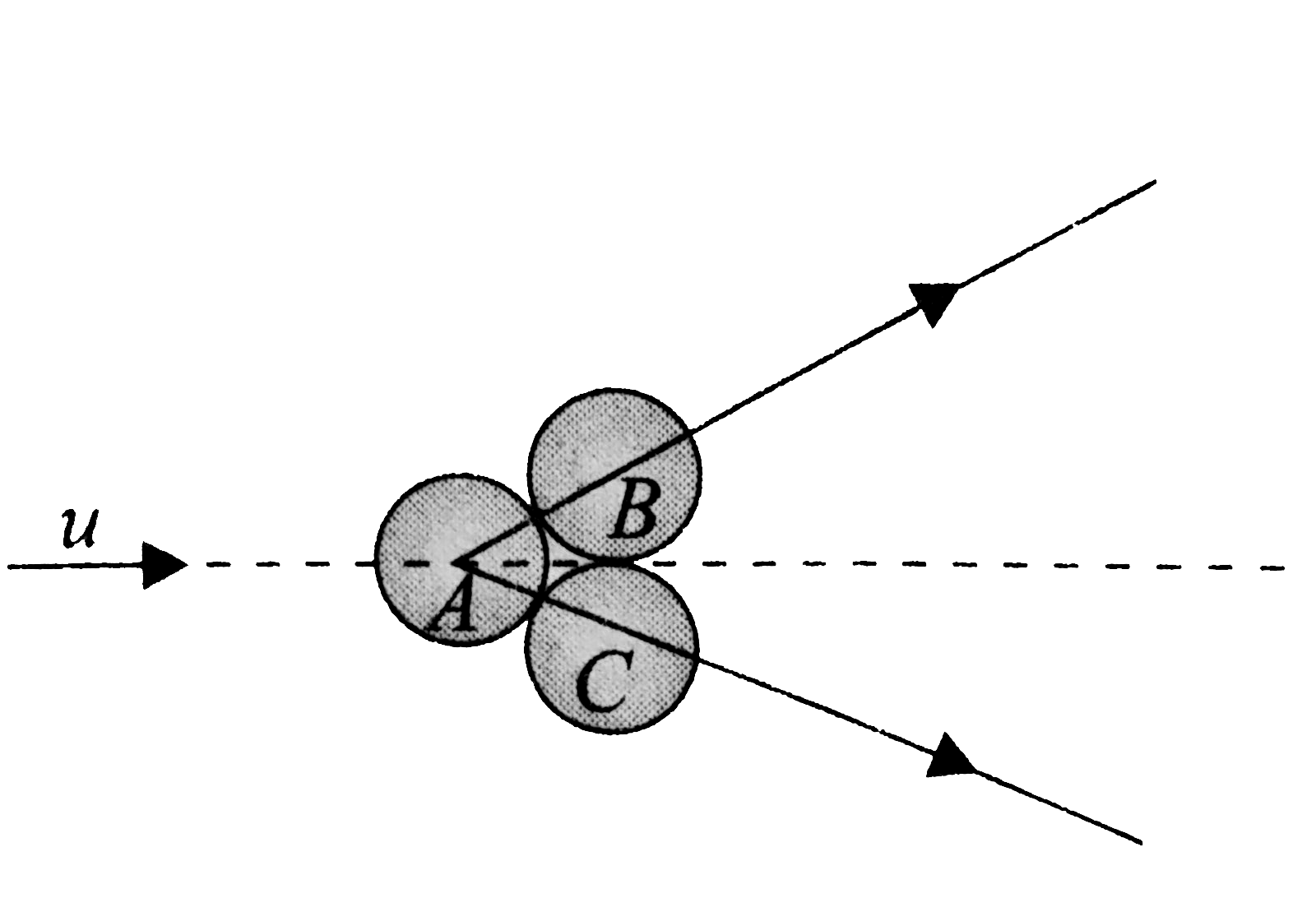
The loss of KE during collision is
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
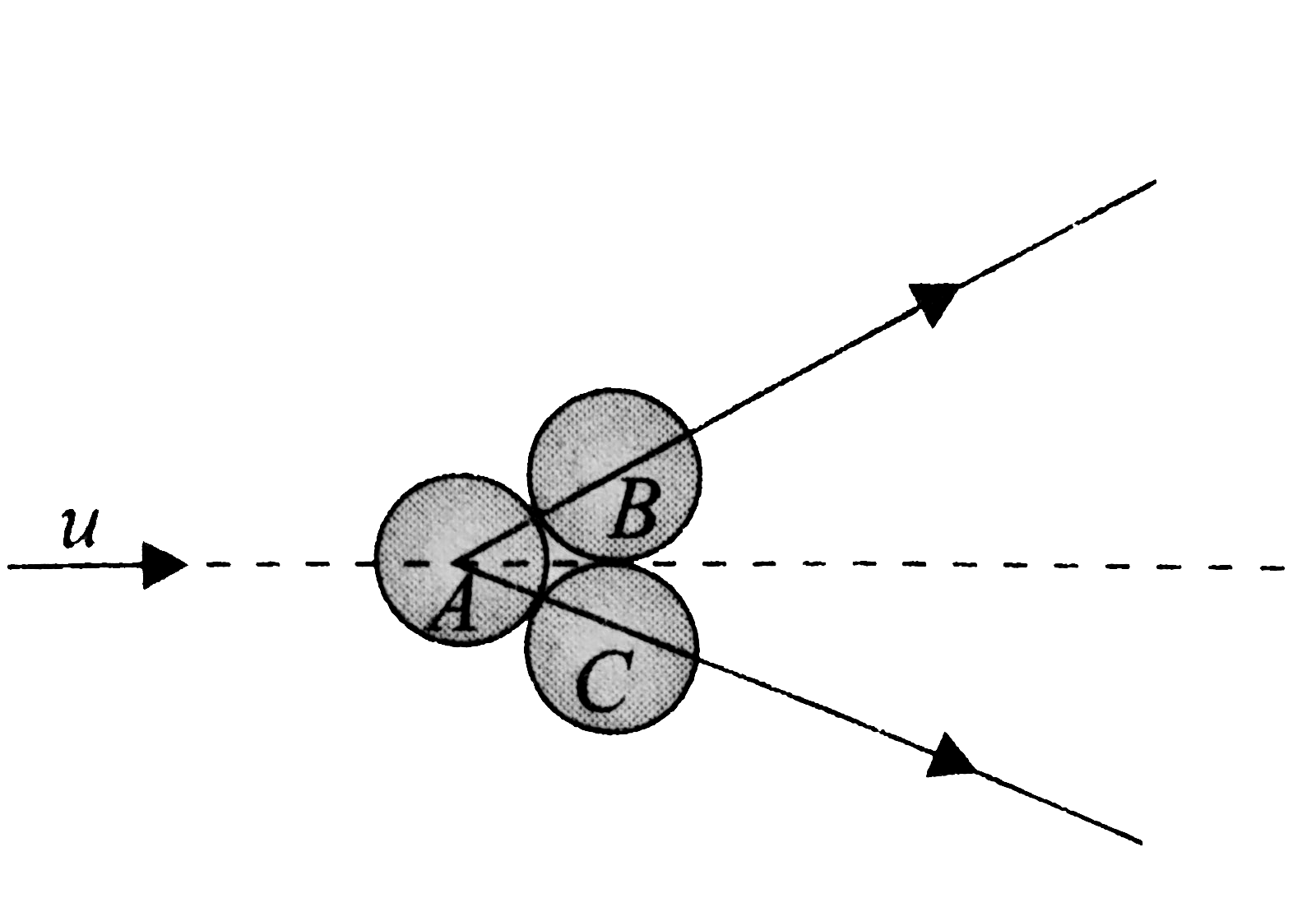
The coefficient of restitution between the two spheres A and B (or between A and C) is
View Solution
Knowledge Check
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass. If e is the coefficient of restitution, then ratio of velocities of the two spheres after collision will be
A1−e1+eB1+e1−eCe+1e−1De−1e+1
Two equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on the and is reduced to rest. Prove that e=23 and find the loss in KE.
View SolutionA body of mass a moving with a velocity b strikes a body of mass c and gets embedded into it. The velocity of the systems after collision is
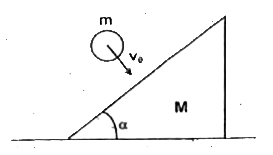
View SolutionA wedge of mass M and angle α rests on a smooth horizontal plane. A smooth sphere of mass m strickes it in a direction perpendicular to its inclined face and rebounds. If the coefficient of restitution is e, find the ratio of the speed of the sphere just before and just after the impact.
View SolutionTwo identical blocks A and B of mass M each are kept on each other on a smooth horizontal plane. There exists friction between A and B. A bullet of mass m hits the the lower block with a horizontal velocity v and goes embedded into it. Find the work done by friction between A and B.
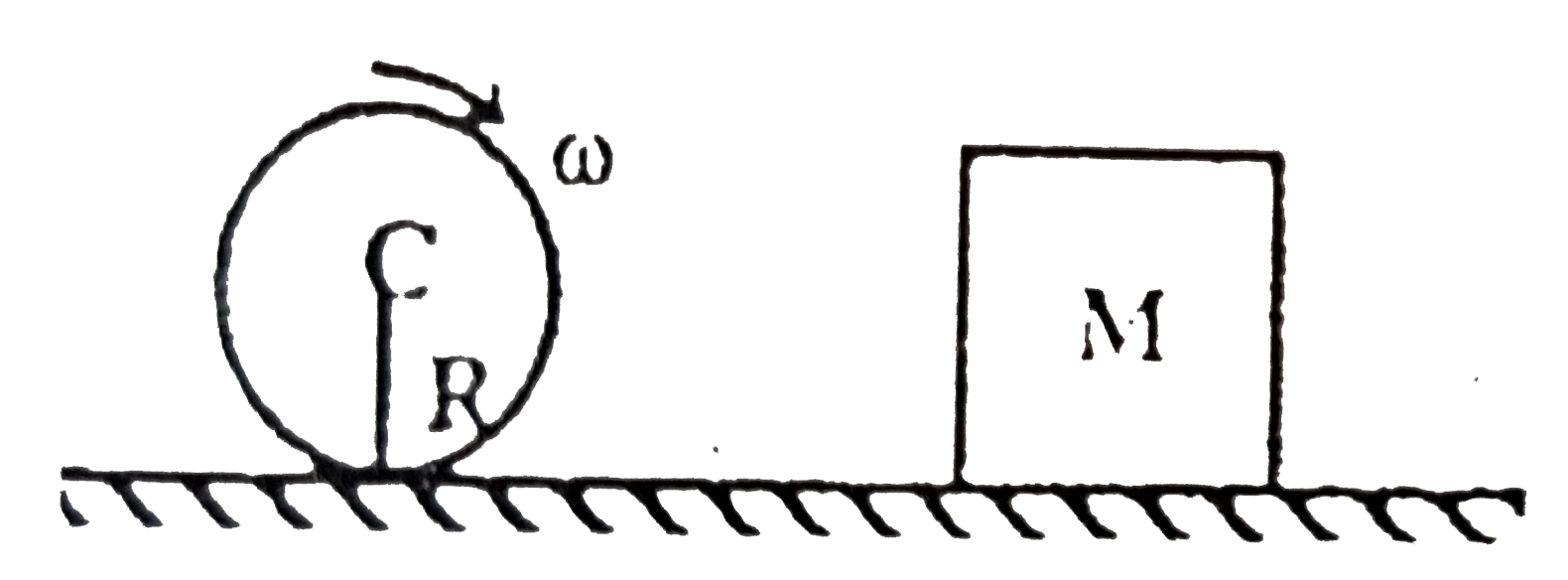
View SolutionA sphere of radius R and mass M collides elastically with a cubical block of mass M and side 2R. The entire system is on a smooth horizontal ground. Given that the sphere was rolling without slipping with an angular velocity ω at the time of collision. The velocities of the sphere and the block after the collision are
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View Solution
