Two identical blocks A and B of mass M each are kept on each other on a smooth horizontal plane. There exists friction between A and B. A bullet of mass m hits the the lower block with a horizontal velocity v and goes embedded into it. Find the work done by friction between A and B.
The correct Answer is:12Mm2v2(m+2M)2
To solve the problem, we will follow these steps:
Step 1: Understand the system
We have two identical blocks A and B, each with mass M, stacked on top of each other on a smooth horizontal plane. A bullet of mass m strikes the lower block B with a horizontal velocity v and embeds itself into it.
Step 2: Apply the principle of conservation of momentum
Before the collision, the momentum of the system is given by the bullet's momentum since the blocks are at rest. After the bullet embeds into block B, we can consider the combined mass of block B and the bullet.
The initial momentum (before the collision) is:
Pinitial=mv
After the bullet embeds into block B, the total mass moving together is M+m (mass of block B plus the mass of the bullet). Let the common velocity after the collision be v0.
Using conservation of momentum:
mv=(M+m)v0
From this, we can solve for v0:
v0=mvM+m
Step 3: Calculate the initial and final kinetic energy
The initial kinetic energy (KE_initial) of the system is only due to the bullet:
KEinitial=12mv2
The final kinetic energy (KE_final) of the system after the collision (both blocks and the bullet moving together) is:
KEfinal=12(M+m)v20
Substituting v0:
KEfinal=12(M+m)(mvM+m)2
KEfinal=12(M+m)m2v2(M+m)2
KEfinal=12m2v2M+m
Step 4: Calculate the work done by friction
The work done by friction (W_friction) between blocks A and B can be found using the change in kinetic energy of block A. Since block A starts from rest, its initial kinetic energy is 0.
Thus, the work done by friction is:
Wfriction=KEfinal−KEinitial
Wfriction=12m2v2M+m−0
Wfriction=12m2v2M+m
Final Answer
The work done by friction between blocks A and B is:
Wfriction=12m2v2M+m
---
We have two identical blocks A and B, each with mass M, stacked on top of each other on a smooth horizontal plane. A bullet of mass m strikes the lower block B with a horizontal velocity v and embeds itself into it.
Before the collision, the momentum of the system is given by the bullet's momentum since the blocks are at rest. After the bullet embeds into block B, we can consider the combined mass of block B and the bullet.
Pinitial=mv
mv=(M+m)v0
v0=mvM+m
The initial kinetic energy (KE_initial) of the system is only due to the bullet:
KEinitial=12mv2
KEfinal=12(M+m)v20
KEfinal=12(M+m)(mvM+m)2
KEfinal=12(M+m)m2v2(M+m)2
KEfinal=12m2v2M+m
The work done by friction (W_friction) between blocks A and B can be found using the change in kinetic energy of block A. Since block A starts from rest, its initial kinetic energy is 0.
Wfriction=KEfinal−KEinitial
Wfriction=12m2v2M+m−0
Wfriction=12m2v2M+m
The work done by friction between blocks A and B is:
Wfriction=12m2v2M+m
Similar Questions
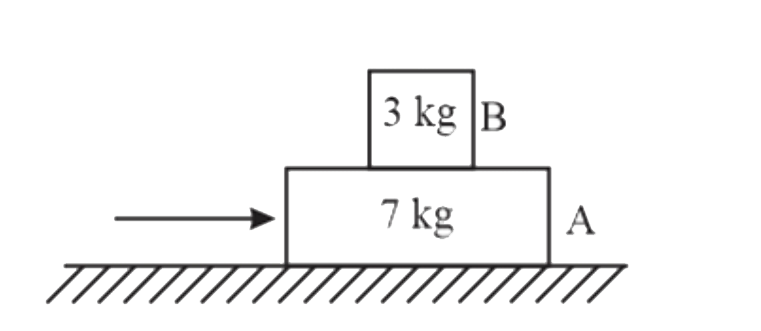
A block A of mass 2kg rests on another block B of mass 8kg which rests on a horizontal floor. The coefficient of friction between A and B is 0.2 while that between B and floor is 0.5.When a horizontal floor F of 25N is applied on the block B the force of friction between A and B is
View SolutionA block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View SolutionThree indentical uniform blocks of mass m each and length L are placed on a smooth fixed horizontal surface as shown. There is friction between A and B (Friction cofficient μ) while there is no friction between A and C. At the instant shown, that is at t=0, the block A has horizontal velocity of magnitude u towards right, whereas speed of B and C is zero. At the instant block A has covered a distance L relative to block B velcity of all blocks are same.
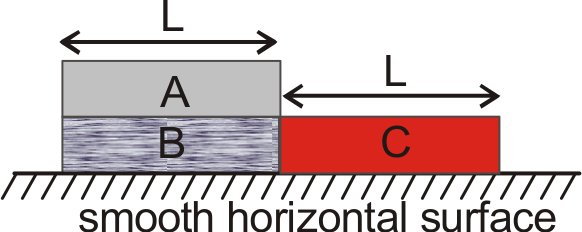
The magnitude of total work done by friction on system of three blocks is
View SolutionTwo blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the lower block A, so that A and B move without separation is 49N. The coefficient of friction between A and B is (take g = 9.8ms−2 )
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
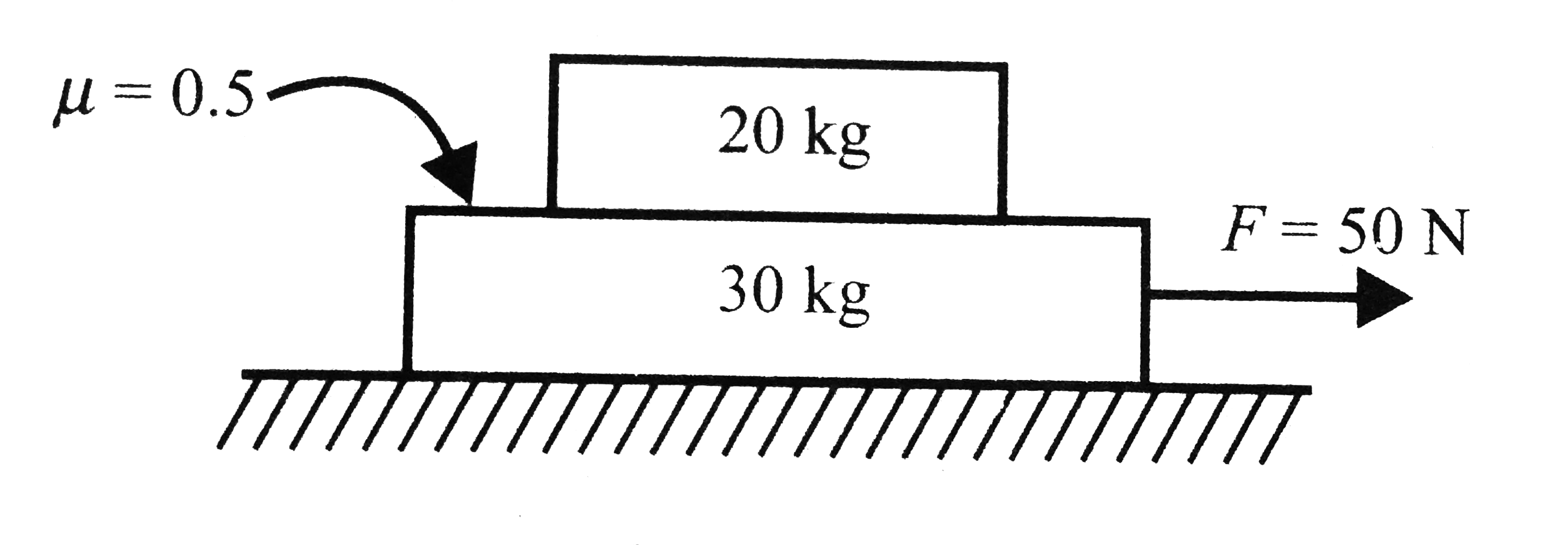
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is

View Solution
