Two fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
The correct Answer is:a. centre at (5 a, 0) and radius 4a
b. (##BMSV03C03E01056_A01##)
c. √14πε0(Qq2ma)
a. Let P be a point in the xy plane with coordinates (x,y) at which the potential due to charges −2Qand+Q placed A and B, respectively, be zer (Fig. S3.24).
(##BMS_V03_C03_E01_056_S01##).
VP=K(−2Q)√(3a+x)2+y2+K(+Q)√(3a−x)2+y2=0
or 2√(3a−x)2+y2=√(3a+x)2+y2
or 4[(3a−x)2+y2]=[(3a+x)2+y2]
or (x−5a)2+(y−0)2=(4a)2
This is the equation of a circle with center at (5a,0) and radius 4a. Thus, c(5a,0) is the center of the circle, where potential is zero.
b. Let us find potential at various points on the x - axis.
For x>3a,
V=kQx−3a−k2Qx+3a=kQ(9a−x)x2−9a2
We see that at x=9a,V=0
For −3a<x<3a,
V=kQ3a−x−k2Qx+3a=kQ3(x−1)9a2−x2
We see that at x=a,V=0.
For x<−3a,
V=kQ3a−x+k(−2Q)−3a−x=−kQ(9a−x)x2−9a2
We see that V≠0 for x<−3a and V is always negative for x<−3a.
c. Applying energy conservation, we get
(KE+PE)center=(KE+PE)circumference
or 0+K[Qq2a−2Qq8a]=12mv2+k[Qq6a−2Qq12a]
or 12mv2=KQq4a or v=√KQq2ma=√14πε0(Qq2ma)
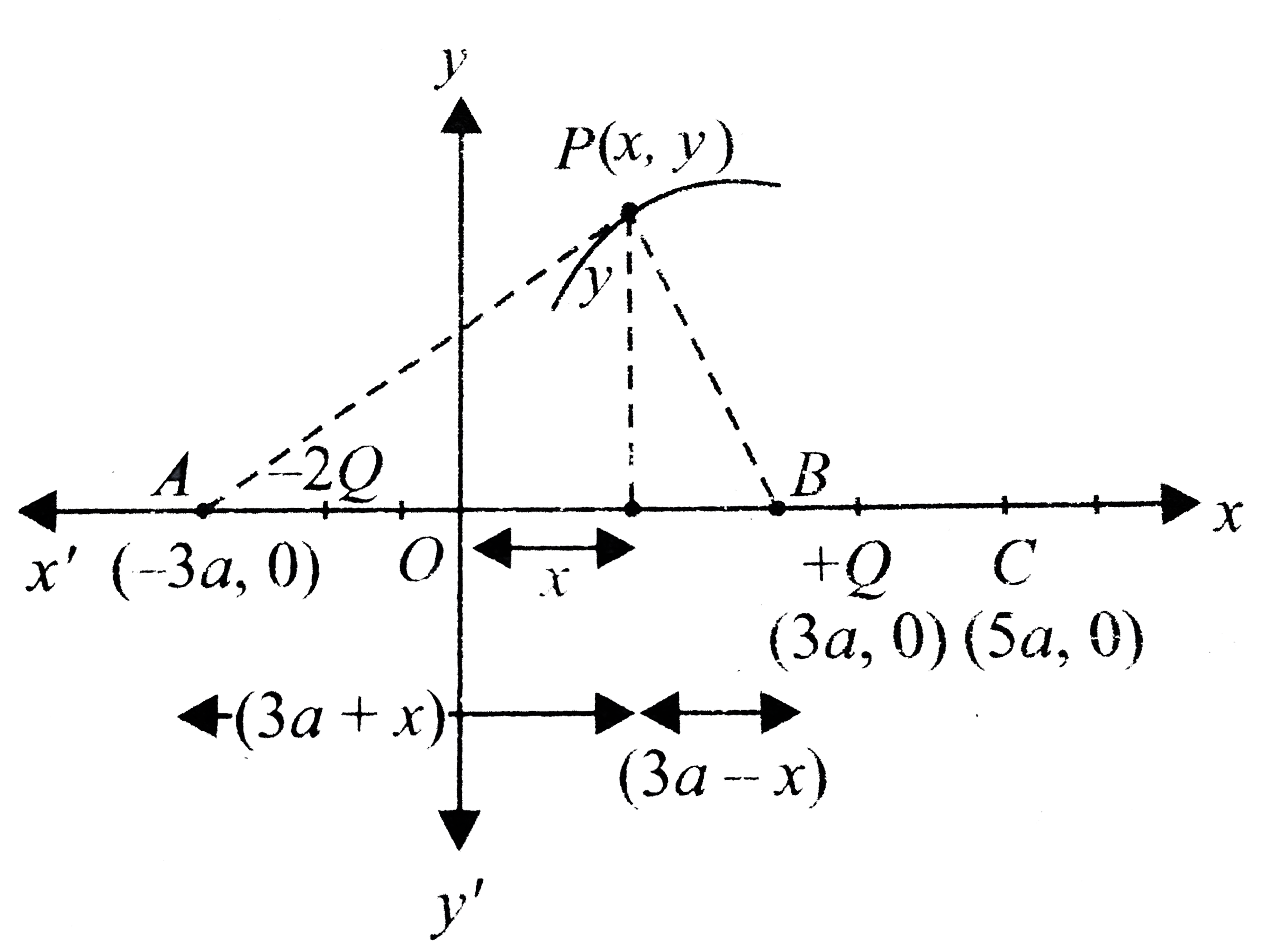 .
.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Single Correct
56 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.3
9 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
Show that all points in the x-y plane where the electric potential due to the two charge is zero , lie on a circle. If its radius is r = xa and the location of its centre is (ya,0) find x and y .
View SolutionTwo fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
If a particle of charge +q starts from rest at the centre of the circle , show by a short quantitavtive argument that the particle eventually crosses the circle . If its speed V=√Qqzπε0ma , then find z.
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo charges of magnitude −2Qand+Q are located at points (a,0)and(4a,0) respectively .
What is the electric flux due to charges through a sphere of radius '3a' with its center at the origin.
View SolutionTwo charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
View Solution(i) Can two equaipotential surfaces intersect each other ? Give reasons
(ii) Two charges −qand+q are located at point A (0, 0 -a) and B(0, 0, +a) respectively. How much work is done in moving a test charge from point P(7,0,0) to Q(−3,0,0) ?
View Solution(i) Can two equpotential surfaces intersect each other ? Give reason.
(ii) Two charges +qand−q are located at points A (0,0,−2)andB(0,0,2) respectively. How much work will be done in moving a test charge from point P(4,0,0) to (−5,0,0) ?
View SolutionTwo point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View Solution
