Two forces are such that the sum of their magnitudes is 18 N, the resultant is √228 when they are at 120∘. Then the magnitude of the forces are
12N,6N
13N,5N
10N, 9N
16N, 2N
The correct Answer is:D
To solve the problem, we need to find the magnitudes of two forces p and q given the following conditions:
1. The sum of their magnitudes is p+q=18N.
2. The resultant of the two forces when they act at an angle of 120∘ is R=√228N.
Step 1: Set up the equations
From the problem, we have:
- p+q=18 (1)
- The formula for the resultant of two forces is given by:
R=√p2+q2+2pqcosθ
where θ=120∘ and cos120∘=−12.
Step 2: Substitute the values into the resultant formula
Substituting R=√228 and cos120∘=−12:
√228=√p2+q2−pq
Step 3: Square both sides to eliminate the square root
Squaring both sides gives:
228=p2+q2−pq(2)
Step 4: Substitute q from equation (1) into equation (2)
From equation (1), we can express q in terms of p:
q=18−p
Substituting this into equation (2):
228=p2+(18−p)2−p(18−p)
Step 5: Expand and simplify the equation
Expanding (18−p)2:
(18−p)2=324−36p+p2
Now substituting back into the equation:
228=p2+(324−36p+p2)−(18p−p2)
Combine like terms:
228=p2+324−36p+p2−18p+p2
This simplifies to:
228=3p2−54p+324
Step 6: Rearrange the equation
Rearranging gives:
3p2−54p+324−228=0
3p2−54p+96=0
Step 7: Divide the entire equation by 3
p2−18p+32=0
Step 8: Factor the quadratic equation
Factoring gives:
(p−16)(p−2)=0
Thus, the solutions for p are:
p=16orp=2
Step 9: Find corresponding q values
Using p+q=18:
1. If p=16, then q=18−16=2.
2. If p=2, then q=18−2=16.
Conclusion
The magnitudes of the forces are 16N and 2N.
2. The resultant of the two forces when they act at an angle of 120∘ is R=√228N.
From the problem, we have:
- p+q=18 (1)
- The formula for the resultant of two forces is given by:
R=√p2+q2+2pqcosθ
where θ=120∘ and cos120∘=−12.
Substituting R=√228 and cos120∘=−12:
√228=√p2+q2−pq
Squaring both sides gives:
228=p2+q2−pq(2)
From equation (1), we can express q in terms of p:
q=18−p
Substituting this into equation (2):
228=p2+(18−p)2−p(18−p)
Expanding (18−p)2:
(18−p)2=324−36p+p2
Now substituting back into the equation:
228=p2+(324−36p+p2)−(18p−p2)
Combine like terms:
228=p2+324−36p+p2−18p+p2
This simplifies to:
228=3p2−54p+324
Rearranging gives:
3p2−54p+324−228=0
3p2−54p+96=0
p2−18p+32=0
Factoring gives:
(p−16)(p−2)=0
Thus, the solutions for p are:
p=16orp=2
Using p+q=18:
1. If p=16, then q=18−16=2.
2. If p=2, then q=18−2=16.
The magnitudes of the forces are 16N and 2N.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-2 (Lami.s theorem :)
8 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-2 ( Relative velocity)
15 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Circular motion)
12 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Two forces are such that the sum of their magnitudes is 18N and their resultant is 12 N which is perpendicular to the smaller force. Then the magnitude of the forces are
View SolutionWhen two vectors of magnitudes P and Q are inclined at an angle θ, the magnitudes of their resultant is 2P. When the inclination is changed to 180∘−θ, the magnitudes of the resultant is halved. Find the ratio of P and Q.
View SolutionThe sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
View SolutionThe sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
View SolutionTwo forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionFind the magnitude of the resultant of shown forces :-
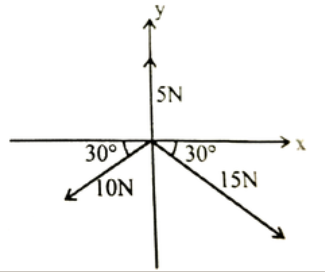
View SolutionTwo forces P and Q acting at a point are such that if P is reveserd, the direction of the resultant is turned through 90∘. Prove that the magnitudes of the forces are equal.
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, What are the magnitudes of forces?
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, What are the magnitudes of forces?
View SolutionTwo forces whose magnitudes are in the ratio 3:5 give a resultant of 28N. If the angle of their inclination is 60∘, find the magnitude of each force.
View Solution
