Two forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
The correct Answer is:PQ=2
To solve the problem, we will follow these steps:
Step 1: Write the equation for the resultant of two forces at angle θ
The magnitude of the resultant R of two forces P and Q inclined at an angle θ is given by:
R=√P2+Q2+2PQcosθ
Step 2: Set up the equation for the first case
According to the problem, when the angle is θ, the resultant is 3Q:
3Q=√P2+Q2+2PQcosθ
Squaring both sides, we get:
(3Q)2=P2+Q2+2PQcosθ
This simplifies to:
9Q2=P2+Q2+2PQcosθ
Rearranging gives:
P2+2PQcosθ=9Q2−Q2
P2+2PQcosθ=8Q2(Equation 1)
Step 3: Set up the equation for the second case
When the angle changes to 180∘−θ, the resultant becomes Q:
Q=√P2+Q2−2PQcosθ
Squaring both sides, we have:
Q2=P2+Q2−2PQcosθ
Rearranging gives:
P2−2PQcosθ=Q2−Q2
P2−2PQcosθ=0
This can be rewritten as:
P2=2PQcosθ(Equation 2)
Step 4: Substitute Equation 2 into Equation 1
Now we substitute P2 from Equation 2 into Equation 1:
2PQcosθ+2PQcosθ=8Q2
This simplifies to:
4PQcosθ=8Q2
Dividing both sides by 4Q (assuming Q≠0):
Pcosθ=2Q
Thus, we can express P in terms of Q:
P=2Qcosθ
Step 5: Find the ratio of the forces
To find the ratio PQ:
PQ=2cosθ
However, we need to find a specific ratio. From the previous equations, we have P2=2PQcosθ. Substituting P=2Q gives us:
(2Q)2=2(2Q)Qcosθ
4Q2=4Q2cosθ
This implies cosθ=1, which means θ=0∘ or P=2Q.
Thus, the ratio of the forces P and Q is:
PQ=2:1
Final Answer
The ratio of the forces P and Q is 2:1.
---
The magnitude of the resultant R of two forces P and Q inclined at an angle θ is given by:
R=√P2+Q2+2PQcosθ
According to the problem, when the angle is θ, the resultant is 3Q:
3Q=√P2+Q2+2PQcosθ
Squaring both sides, we get:
(3Q)2=P2+Q2+2PQcosθ
This simplifies to:
9Q2=P2+Q2+2PQcosθ
Rearranging gives:
P2+2PQcosθ=9Q2−Q2
P2+2PQcosθ=8Q2(Equation 1)
When the angle changes to 180∘−θ, the resultant becomes Q:
Q=√P2+Q2−2PQcosθ
Squaring both sides, we have:
Q2=P2+Q2−2PQcosθ
Rearranging gives:
P2−2PQcosθ=Q2−Q2
P2−2PQcosθ=0
This can be rewritten as:
P2=2PQcosθ(Equation 2)
Now we substitute P2 from Equation 2 into Equation 1:
2PQcosθ+2PQcosθ=8Q2
This simplifies to:
4PQcosθ=8Q2
Dividing both sides by 4Q (assuming Q≠0):
Pcosθ=2Q
Thus, we can express P in terms of Q:
P=2Qcosθ
To find the ratio PQ:
PQ=2cosθ
However, we need to find a specific ratio. From the previous equations, we have P2=2PQcosθ. Substituting P=2Q gives us:
(2Q)2=2(2Q)Qcosθ
4Q2=4Q2cosθ
This implies cosθ=1, which means θ=0∘ or P=2Q.
PQ=2:1
The ratio of the forces P and Q is 2:1.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Single Correct
51 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
When two vectors of magnitudes P and Q are inclined at an angle θ, the magnitudes of their resultant is 2P. When the inclination is changed to 180∘−θ, the magnitudes of the resultant is halved. Find the ratio of P and Q.
View SolutionFind the magnitude of the resultant of shown forces :-
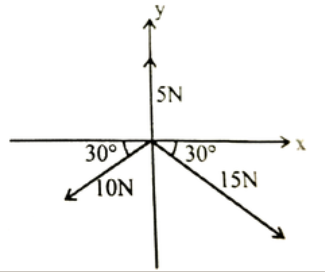
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
Two vectors having magnitude 12 and 13 are inclined at and angle45∘ to each other.find their resultant vector.
View SolutionTwo equal forces of magnitude 'p' each are angled first at 60° later at 120°. The ratio of magnitude of their resultants is
View SolutionTwo forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
View SolutionTwo equal forces (P each) act at a point inclined to each other at an angle of 120∘. The magnitude of their resultant is
View SolutionTwo forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, What are the magnitudes of forces?
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, What are the magnitudes of forces?
View Solution
