Two forces each of magnitude 5 N are applied in opposite directions at the ends of a uniform nod of length 0.5 m. Draw diagram of the arrangement and find the total moment of the two forces.
Step-by-Step Solution
Step 1: Draw the Diagram
Draw a horizontal line to represent the uniform rod. Label the ends of the rod as point A and point B. The length of the rod is 0.5 m. At point A, draw an arrow pointing to the left to represent the force F1 (5 N). At point B, draw an arrow pointing to the right to represent the force F2 (5 N).
Diagram:
A−−−−−−−−−−−−−−B<−−−5N(F1)5N(F2)−−→
Step 2: Identify the Moment Arm
The moment arm (r) is the perpendicular distance from the line of action of the force to the pivot point. In this case, we can take the midpoint of the rod as the pivot point. The distance from the midpoint to either end (A or B) is:
\( r = \frac{0.5 \, \text{m}}{2} = 0.25 \, \text{m} \)
Step 3: Calculate the Moment due to Force F1
The moment (τ1) due to force F1 can be calculated using the formula:
\( \tau_1 = F_1 \times r_1 \)
Where:
- \( F_1 = 5 \, \text{N} \)
- \( r_1 = 0.25 \, \text{m} \)
Substituting the values:
\( \tau_1 = 5 \, \text{N} \times 0.25 \, \text{m} = 1.25 \, \text{N m} \)
Step 4: Calculate the Moment due to Force F2
Similarly, the moment (τ2) due to force F2 can be calculated using the same formula:
\( \tau_2 = F_2 \times r_2 \)
Where:
- \( F_2 = 5 \, \text{N} \)
- \( r_2 = 0.25 \, \text{m} \)
Substituting the values:
\( \tau_2 = 5 \, \text{N} \times 0.25 \, \text{m} = 1.25 \, \text{N m} \)
Step 5: Calculate the Total Moment
Since both forces are acting in opposite directions but create moments in the same direction (clockwise), the total moment (τ) is the sum of the individual moments:
\( \tau = \tau_1 + \tau_2 \)
Substituting the values:
\( \tau = 1.25 \, \text{N m} + 1.25 \, \text{N m} = 2.50 \, \text{N m} \)
Final Answer
The total moment of the two forces is 2.50 N m in the clockwise direction.
---
A−−−−−−−−−−−−−−B<−−−5N(F1)5N(F2)−−→
- \( F_1 = 5 \, \text{N} \)
- \( r_1 = 0.25 \, \text{m} \)
- \( F_2 = 5 \, \text{N} \)
- \( r_2 = 0.25 \, \text{m} \)
Topper's Solved these Questions
Similar Questions
Two forces each of magnitude 2N act vertically upwards and downwards respectively at the two ends of a uniform rod of length 1m which is pivoted at its centre. Draw a diagram of the arrangement and determine the resultant moment of forces about the mid point of the rod.
View SolutionA body is acted upon by two forces each of magnitude F, but in opposite directions. State the effect of the forces if
(a) both forces act at the same point of the body.
(b) the two forces act at two different points of the body at a separation?
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
The forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid point O as shown is fig. 1.30, Determine the magnitude of the resultant moment of forces about the pivot O.

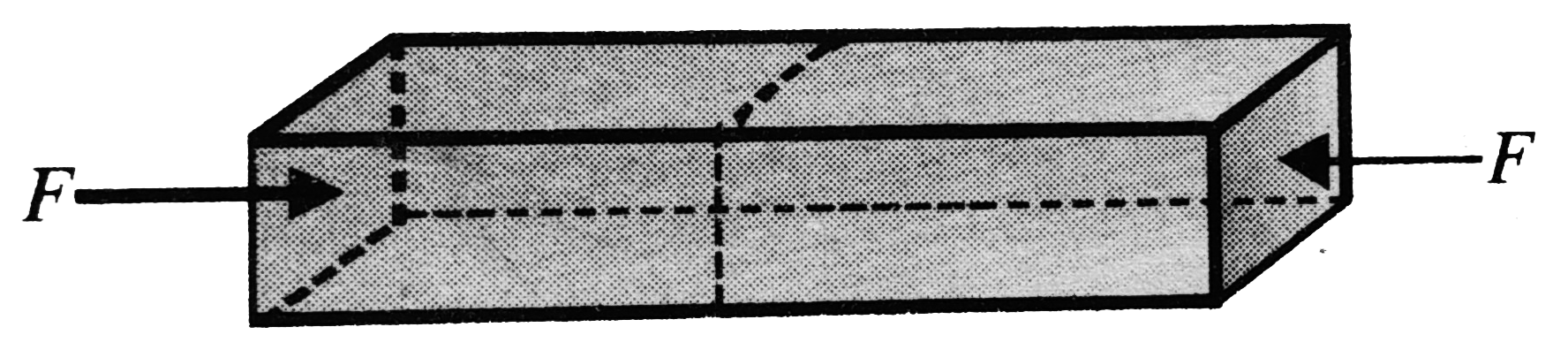
View SolutionIn the figure shown, forces of equal magnitude are applied to the two ends of a uniform rod. Consider A as the cross-sectional area of the rod. For this situation, mark out the incorrect statements.
View SolutionTwo forces, while acting on particle in opposite directions,have the resultant of 10N. If they act at right angles to each other, the resultant is found to be 50N. Find the two forces?
View SolutionTwo perpendicular forces of magnitudes 10 N and 5 N act at a point. Find their resultant.
View SolutionMoment of a force of magnitude 10 N acting along positive y-direction at point (2m,0,0) about the point (0,1m,0) in N-m is
View SolutionMoment of a force of magnitude 20 N acting along positive x-direction at point (3m,0,0) about the point (0,2,0) (in N-m) is
View SolutionA potential difference of 30V is applied between the ends of a conductor of length 100 m and resistance 0.5Ω . The conductor has a uniform cross-section. Find the total linear momentum of free electrons.
View Solution
