Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
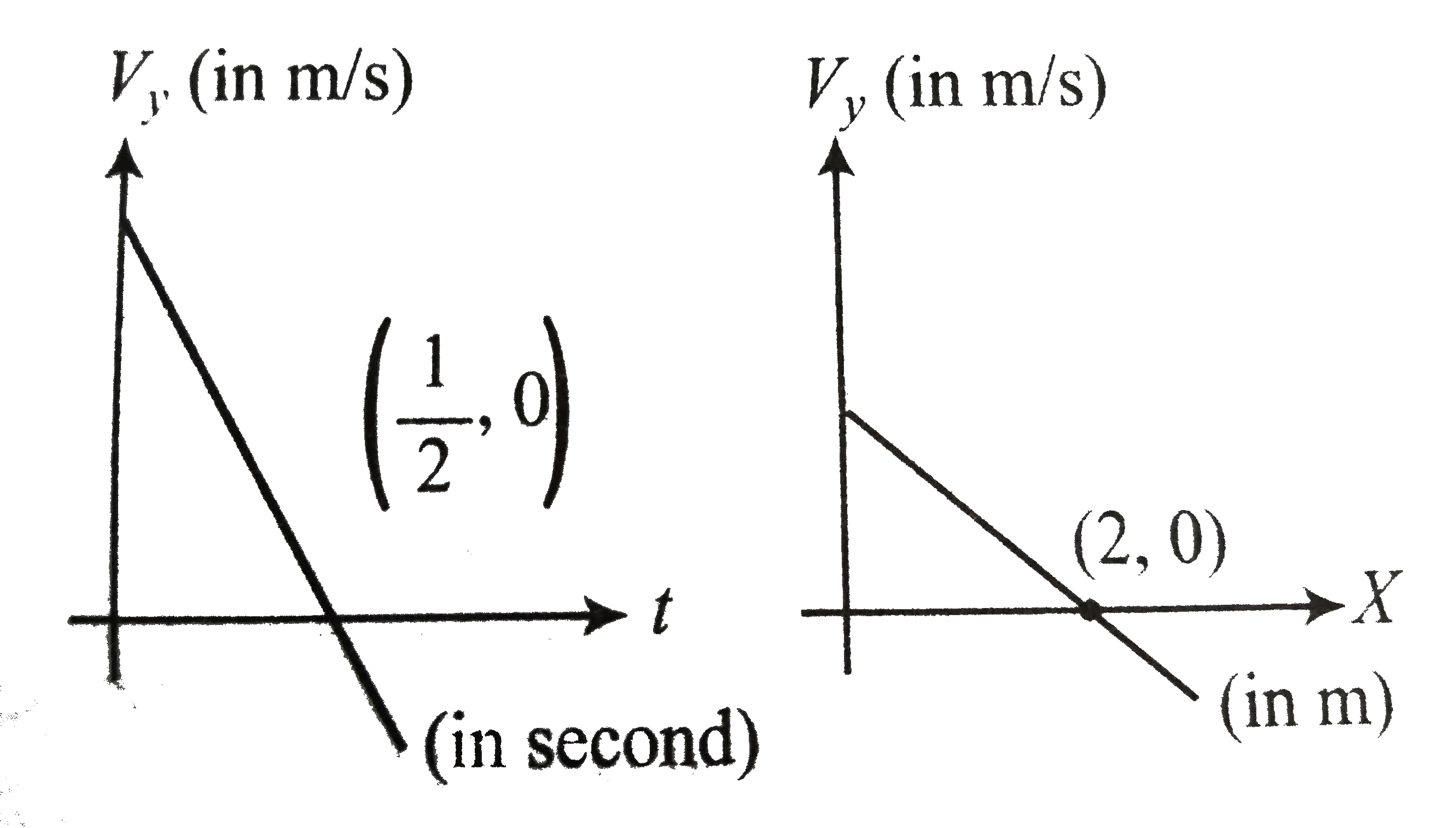 ,
,
Maximum height attained from the point of projection is
1.25 m
12.5 m
2.25 m
None of these
The correct Answer is:A
Time of flight (T) = 1s
2uyg=1s⇒uy=5ms−1
Range (R) = 4m.
(2(ux)(uy)).g=4⇒ux=4ms−1
u=√u2x+u2y=√41ms−1
θ=tan−1(uyux)=tan−1(54)
H=u2y2g=(5)220=54=1.25m.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two graphs of the same projectile motion (in the x - y plane) projected from origin are shown in (Fig. 5 .10). X - axis is along horozontal direction and Y - axis is vertically upwards. Take g=10ms2
Find (i) The y component of initial velocity and
(ii) the X component of initial velocity.
 .
.
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
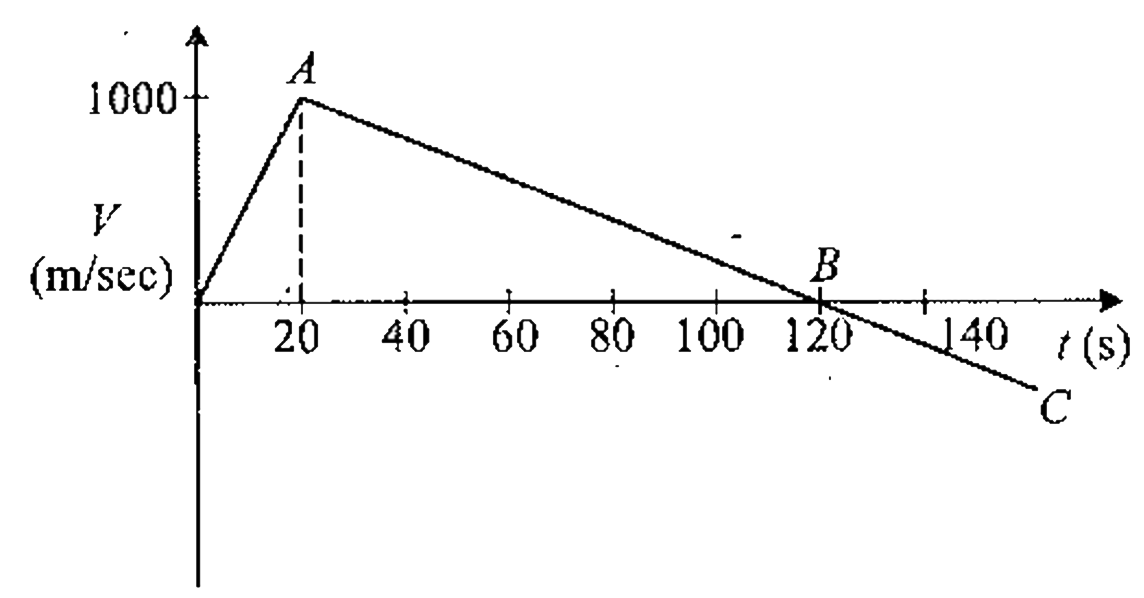
View Solution
Knowledge Check
Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
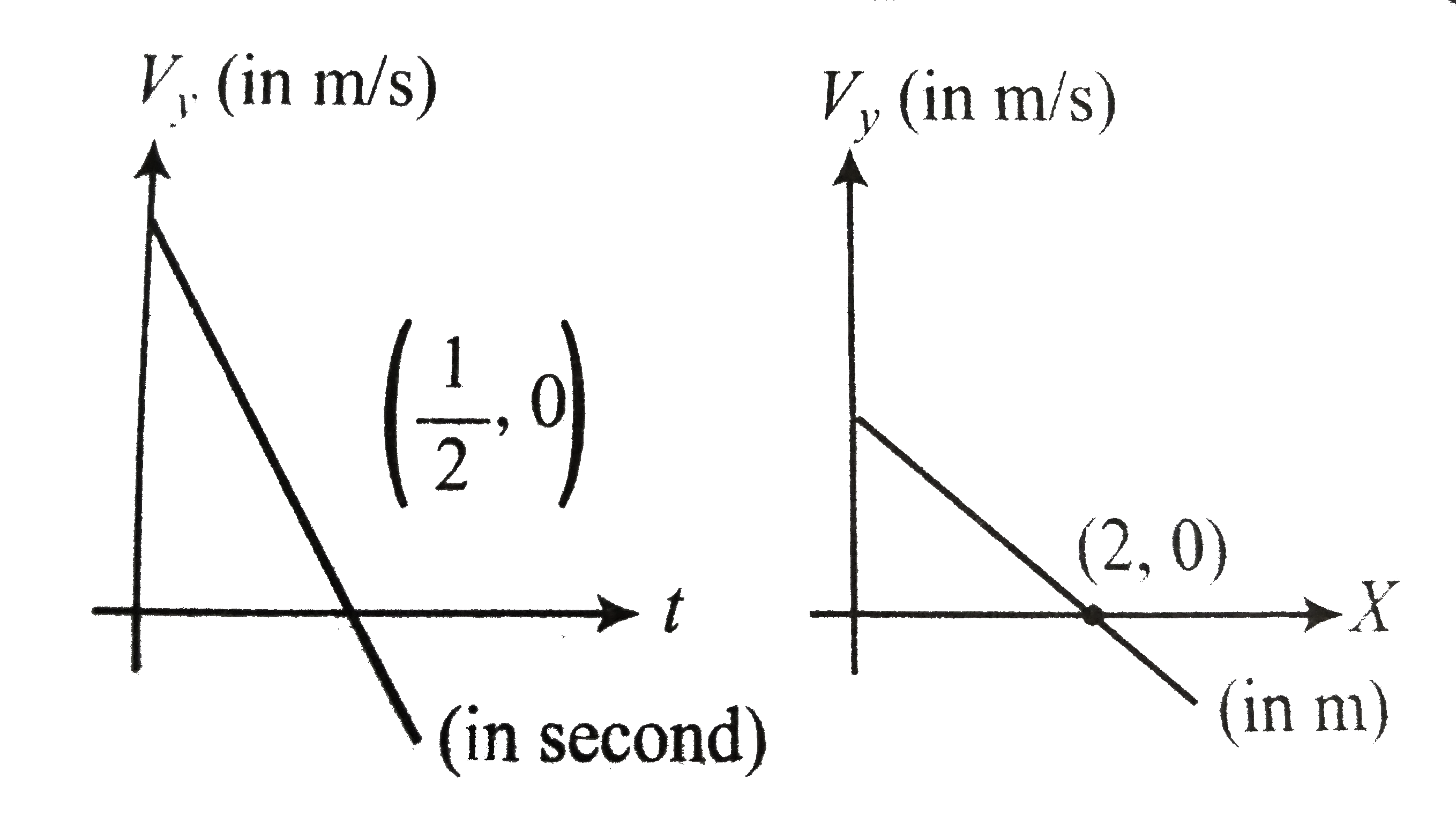 ,
,
The projection speed is :A√37ms−1B√41ms−1C√14ms−1D√40ms−1Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
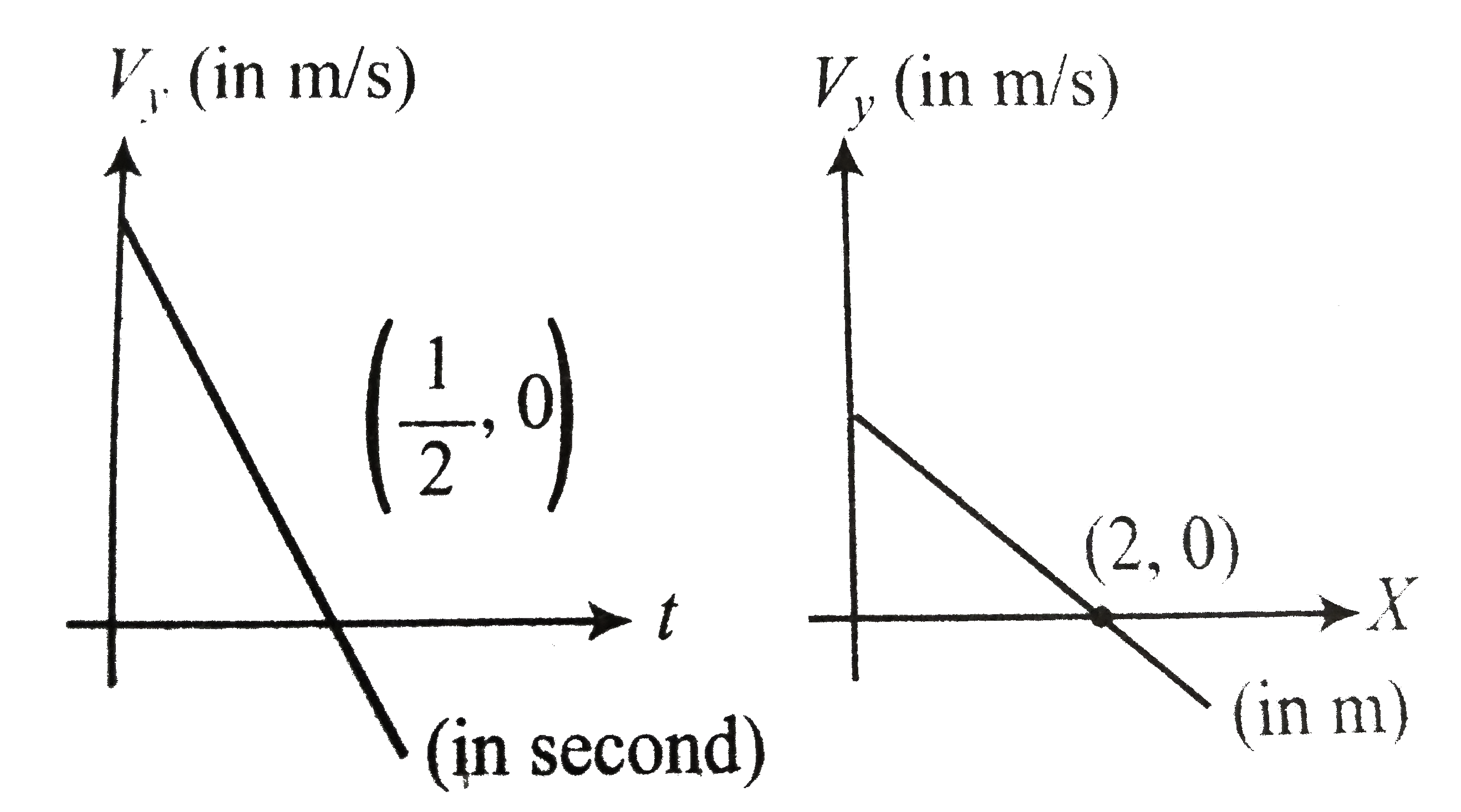
Projection angle with the horizontal is :Atan−1(45)Btan−1(23)Ctan−1(54)Dtan−1(12)For an object projected from ground with speed u horizontal range is two times the maximum height attained by it. The horizontal range of object is
A2u23gB3u24gC3u22gD4u25g
A particle is projected from origin in xy-plane and its equation ,of trajectory is given by y=ax−bx2. The only acceleration ,in the motion is' f' which is constant and in −ve direction of, y-axis.
(a) Find the velocity of projection and the angle of projection.
(b) Point of projection is considered as origin and x-axis along the horizontal ground. Find the horizontal range: and maximum height of projectile. Projectile completes its flight in horizonal plane of projection.
View SolutionA projectile is thrown from ground at a speed v0 at an angle α to the horizontal. Consider point of projection as origin, horizontal direction as X axis and vertically upward as Y axis. Let t be the time when the velocity vector of the projectile becomes perpendicular to its position vector.
(a) Write a quadratic equation in t.
(b) What is the maximum angle a for which the distance of projectile from the point of projection always keeps on increasing? [Hint: Start from the equation you obtained in part (a)]
View SolutionA particle is projected from the ground . Point of projection is taken as origin, horizontal direction as X-axis and verticle upward direction ass Y-axis. Equation of trajectory of the partcle is y=αx−βx2. Horizontal range of the projectile is
View SolutionA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
View SolutionAt a height of 0.4 m from the ground, the velocity of projectile in vector from is →u=(6ˆi+2ˆj) (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is : (g=10m/s2)
View Solution
