Two guns situated at the top of a hill of height 10m fire one shot each with the same speed 5√3m/s at some interval of time. One gun fires horizontal and the other fores upwards at an angle of 60∘ with the horizontal. Two shots collide in air at a poit P. Find (i) time-interval between the firing and (ii) coordinates of the point P. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the x−y plane.
As shown in Fig. 5.43, from equation of motion
s=−s0+ur+12at2 for first gun,
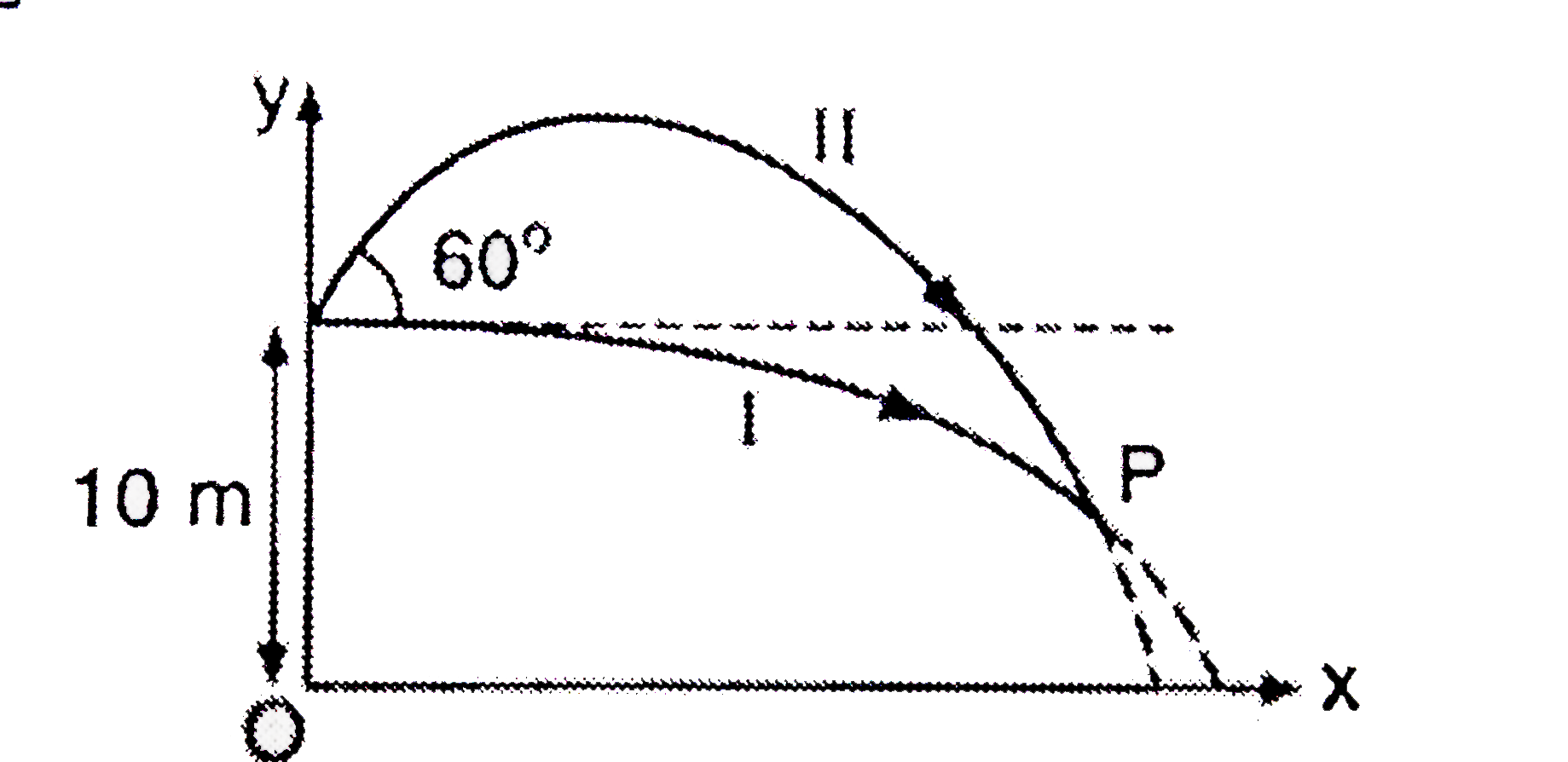
x1=5√3t1 ......(i)
and y1=10−12>21 .........(ii)
While for the second gun
x2=5√3cos60∘t2 ........(iii)
and y2=10+5√3sin60∘t2−12>22
For collision
x1=x2 and y1=y2
i.e.,5√3t1=5√312t2 and 10−12>21=10+152t2−12>22
i.e., t2=2t1 and g(t22−t21)=15t2
Which on simplification gives t1=1 sec and t2=2 sec.
So, the interval between the firings =2-1=1 sec and substituting t1=1 s and g=10 m/2 in Eqns. (i) and (ii) co-ordinates of point P will be (5√3,5)m.
Topper's Solved these Questions
Similar Questions
Two guns situated at the top of a hill of height 10m fire one shot each with the same speed 5√3m/s at some interval of time. One gun fires horizontal and the other fores upwards at an angle of 60∘ with the horizontal. Two shots collide in air at a poit P. Find (i) time-interval between the firing and (ii) coordinates of the point P. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the x−y plane.
View SolutionTwo guns are situated at the top of a hill firing the shots at the same speed. One gun fires the shot horizontally and other gun fires the shot at an angle of 60∘ with horizontal. Two two shots collide in air. If the time taken by horizontal shot to reach the point of collision in 3seconds, find the time interval between two shots.
View Solution
Knowledge Check
At t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.
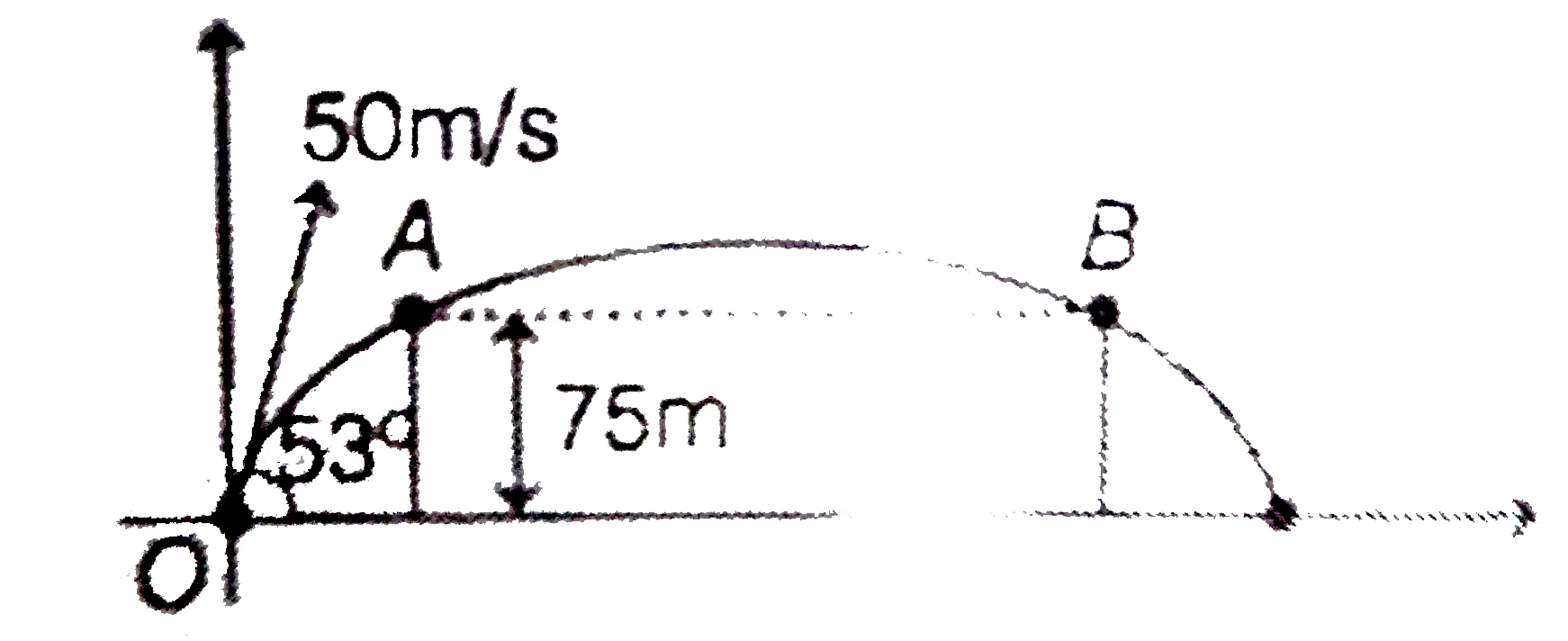
The horizontal separation between the points A and BA30mB60mC90mDnone of theseA shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
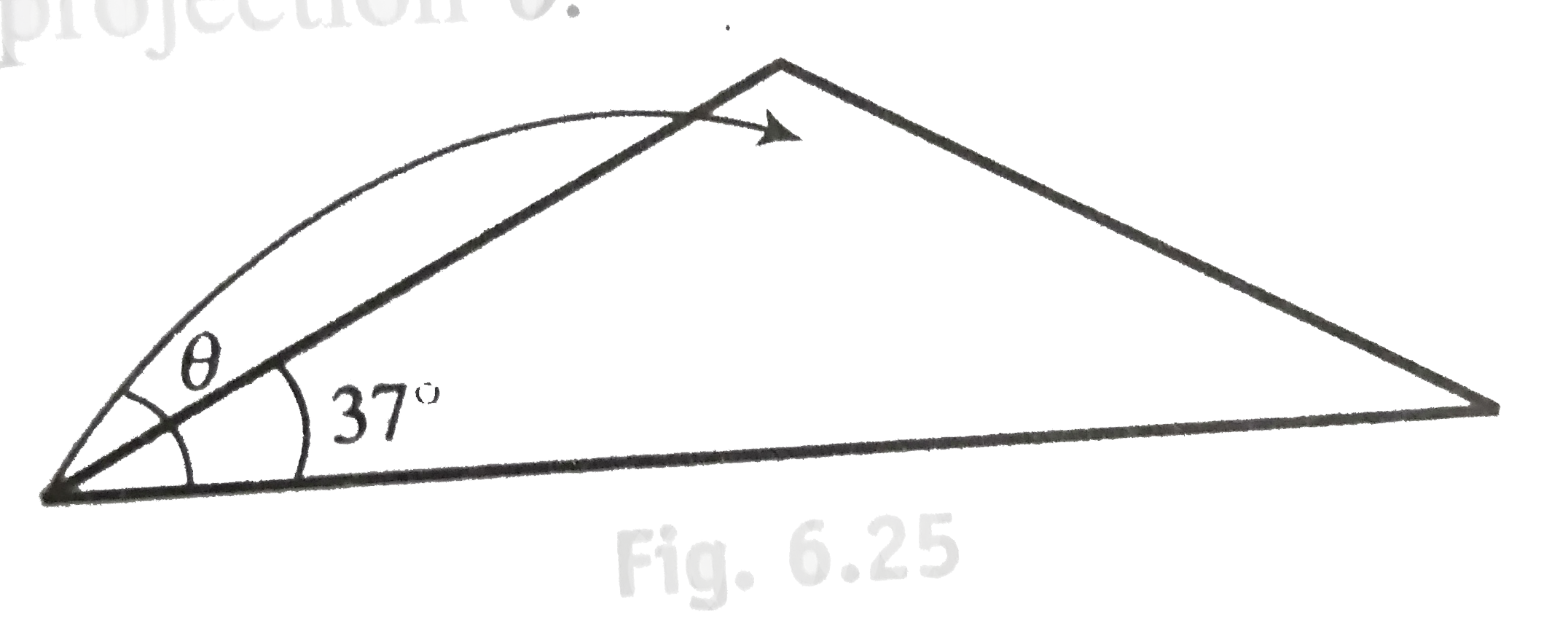 Atanθ=25Btanθ=38Ctanθ=32DNone of these
Atanθ=25Btanθ=38Ctanθ=32DNone of theseA shot is fired at an angle α to the horizontal up a hill of inclination β to the horizontal. Then it strikes the hill horizontally if
Atanα=2tanβBtanα=tanβCtanα.tanβ=1DNone
A bullet is fired with speed 50m/s at 45∘ angle with horizontal. Find the height of the bullet when its direction of motion makes angle 30∘ with the horizontal.
View SolutionA gun fires a shell and recoils horizontally . If the shell travels along the barrel with speed v , the ratio of speed with which the gun recoils if (i) the barrel is horizontal (ii) inclined at an angle of 30∘ with horizontal is
View SolutionA cannon fires two shells successively with velocity 250ms−1 at angles 60∘ and 45∘ with the horizontal in the same vertical plane one after the other . What should be the interval between the firings so that they may hit the same target simultaneously ?
View SolutionAt t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.

The horizontal separation between the points A and B
View SolutionAt t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.
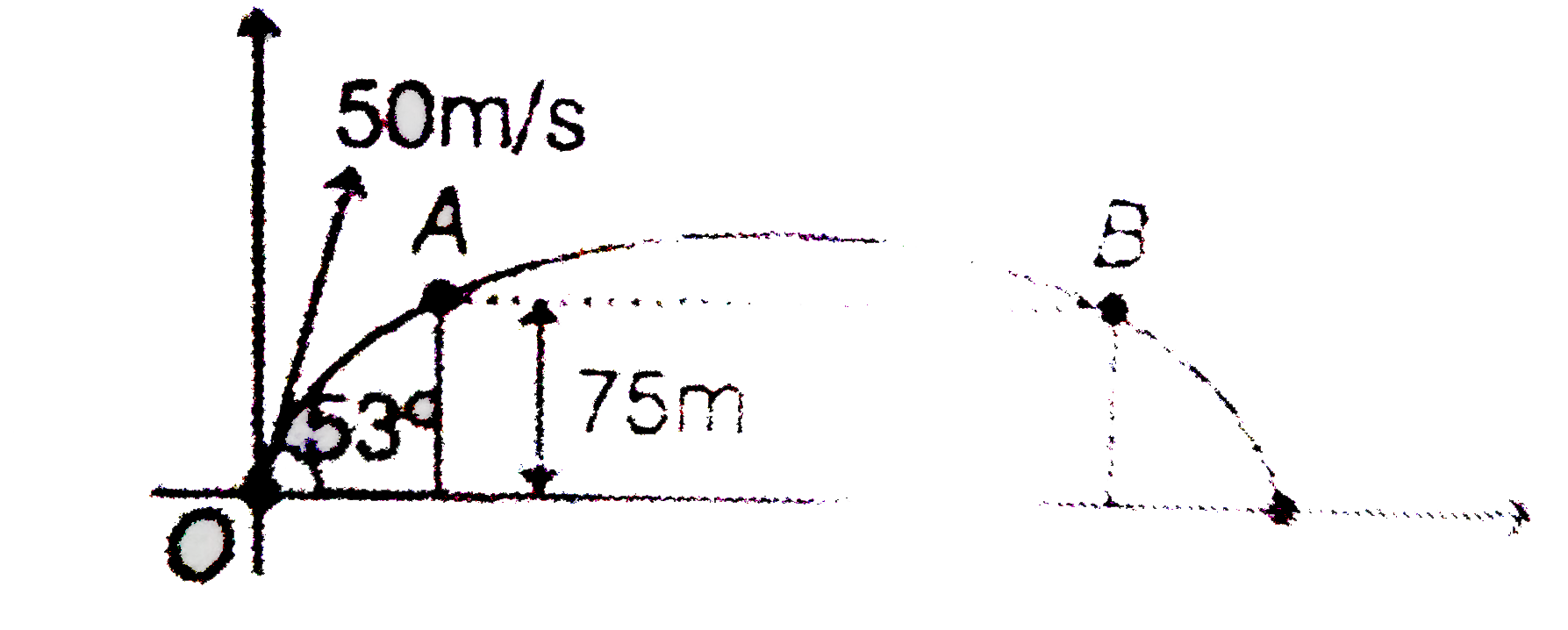
The distance (in metre) of the particle from origin at t=2s
View Solution
