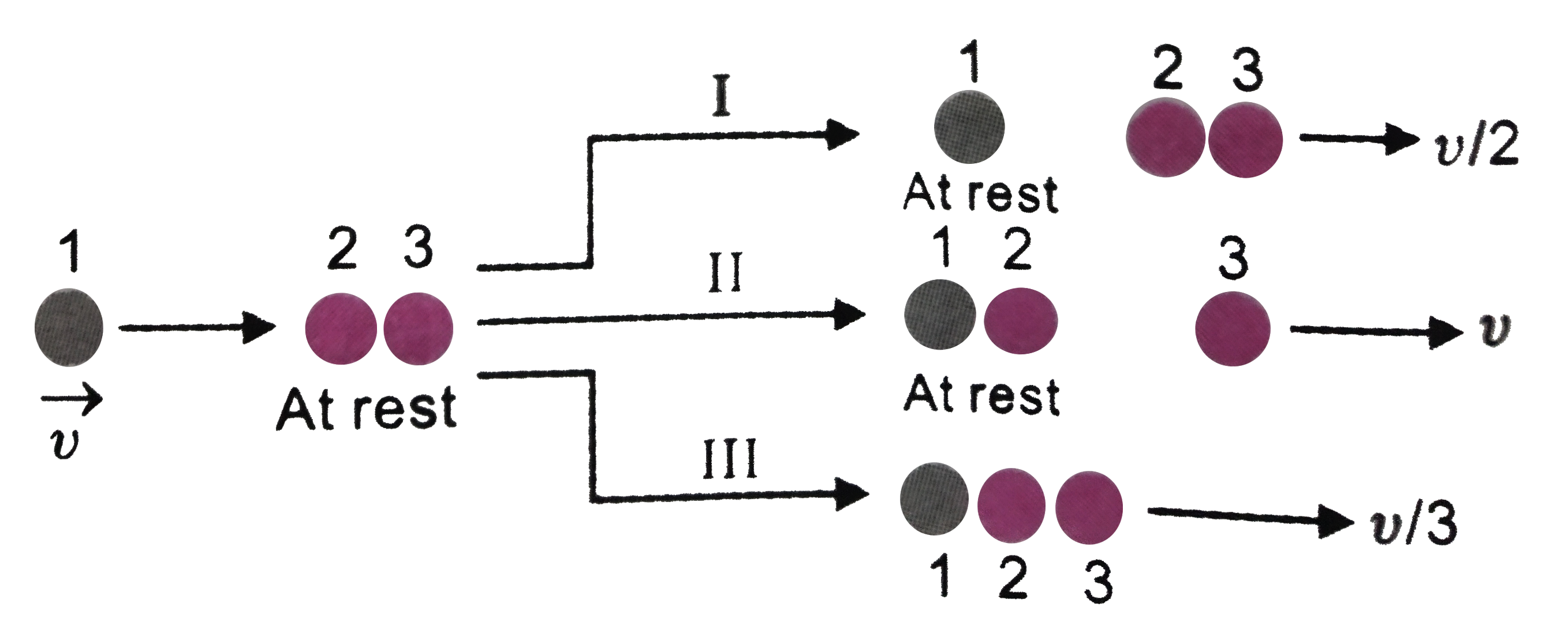
Two identical ball bearings in contact with each other and resting on a frictionless table are hit heat-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
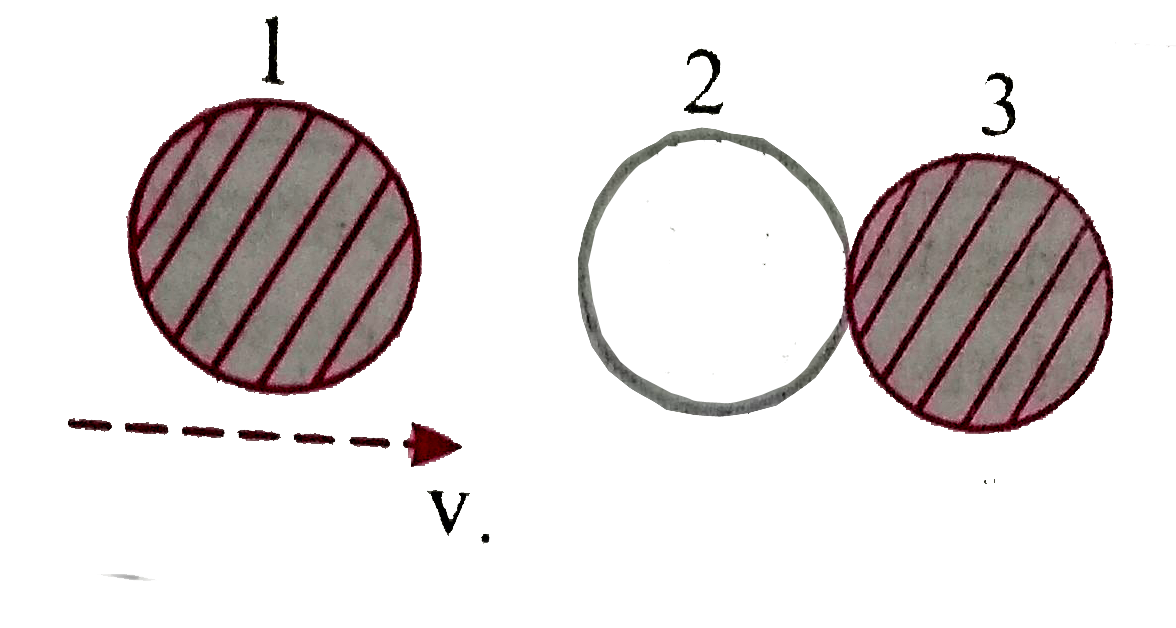
If the collision is elastic, which of the following (figure) is a possible result after collision ?
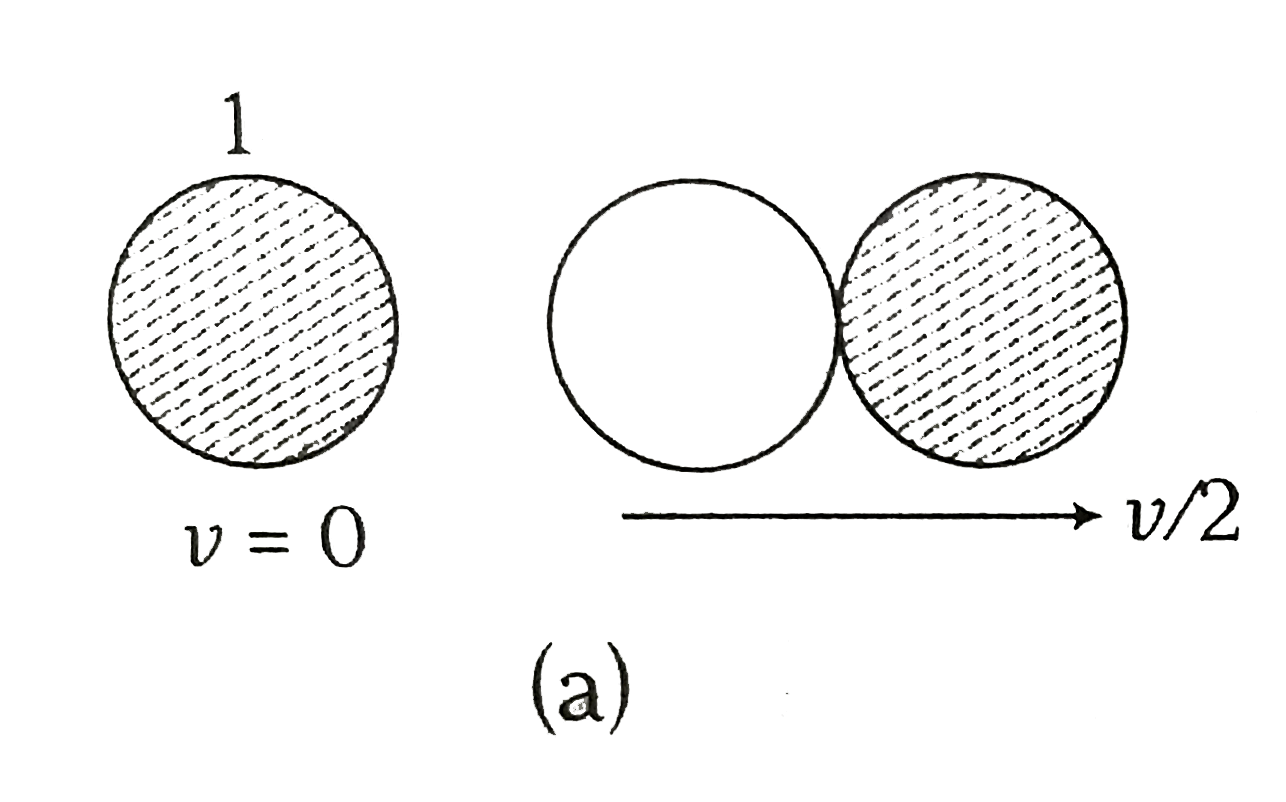

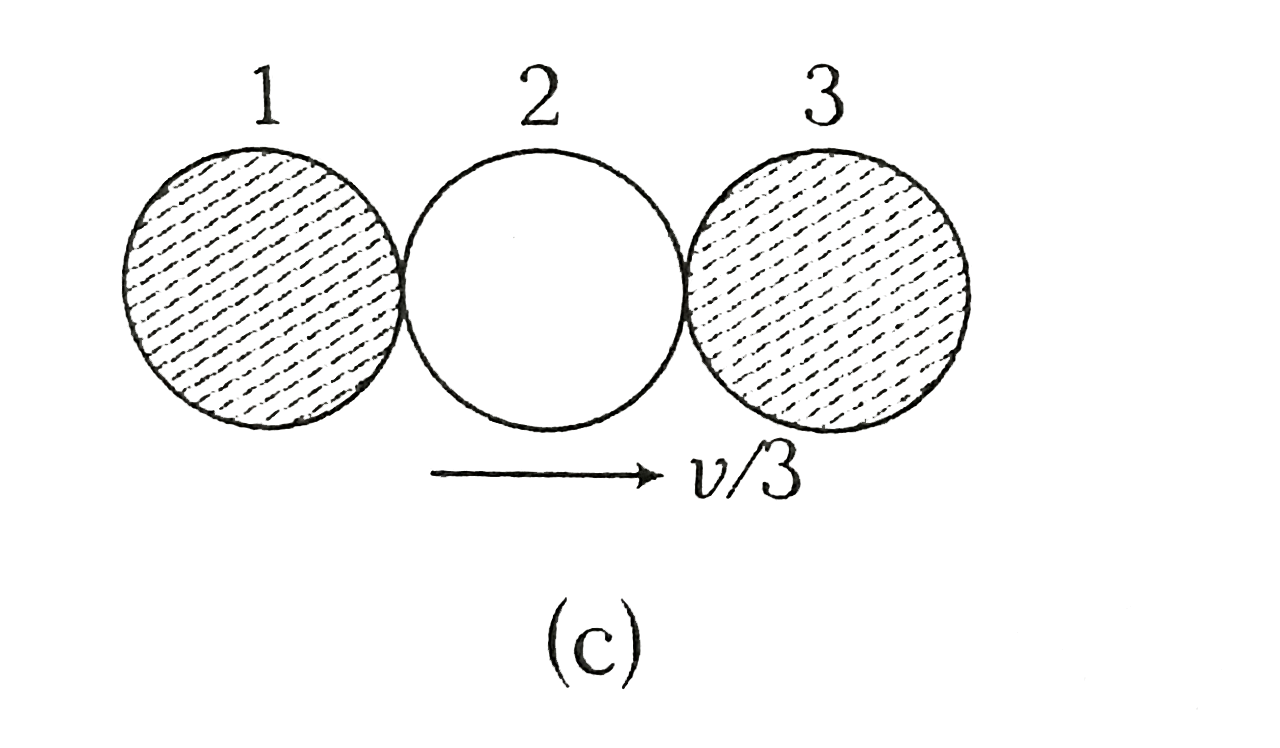
The correct Answer is:B
When two bodies of equal masses collides elastically, their velocities are interchanged.
When ball 1 collides with ball-2, then velocity of ball-1, v1 becomes zero and velocity of ball-2, v2 becomes v, i.e., similarly.
v1=0⇒v2=v
When ball 2 collides will ball 3
v2=0,v3=v
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head on by another ball bearing of the same mass moving initially with a speed v, figure,. If the collision is elastic, which of the following is a possible result after collisioin?
View SolutionTwo identical vehicles are moving with same velocity v towards an intersection as shown in figure. If the collision is completely inelastic, then

View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionIn the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius R/2, is coming down vertically and has a velocity =v0 when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to

View SolutionSTATEMENT - 1 : Two identical balls B and C lie on a horizontal smooth straight groove so that they are touching. A third identical ball A moves at a speed v along the groove. And collides with B as shown in figure. If the collisions are perfectly elastic, then after the collision, balls A and B will come to rest and ball C moves with velocity v to the right.
because

STATEMENT - 2 : In an elastic collision, linear momentum and kinetic energy are both conserved.
View SolutionA ball moving on a horizontal frictionless plane hits an identical ball at rest with a velocity of 0.5m/s. If the collision is elastic, calculate the speed imparted to the target ball, if the speed of projectile after the collision is 30cm/s.
View SolutionA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?

View Solution
