Two identical blocks A and B, each of mass m resting on smooth floor, are connected by a light spring of natural length L and the spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is proportional toSolution in Telugu
√m2k
m√v2k
√mvk
mv2k
The correct Answer is:a
compression,x=VT=Vx2π√m2k
xα√m2k

Topper's Solved these Questions
Similar Questions
Two coherent sources of intensity ratio 9:4 produce interference. The intensity ratio of maxima and minima of the interference pattern is
View SolutionTwo blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
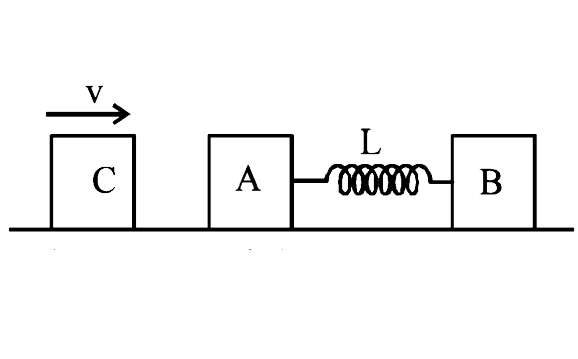
View SolutionTwo blocks A and H . each of mass m , are connected by a massless spring of natural length I . and spring constant K . The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C , also of mass m , moves on the floor with a speed v along the line joining A and B . and collides elastically with A . Then
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
View SolutionBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in figure below. A third identical bloack C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides with A. Then :

View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k. A third body C of mass m moves with velocity v_(0) along the line joining A and B and collides elastically with A. If l_(o) be the natural length of the spring then find the minimum separation between the blocks.
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
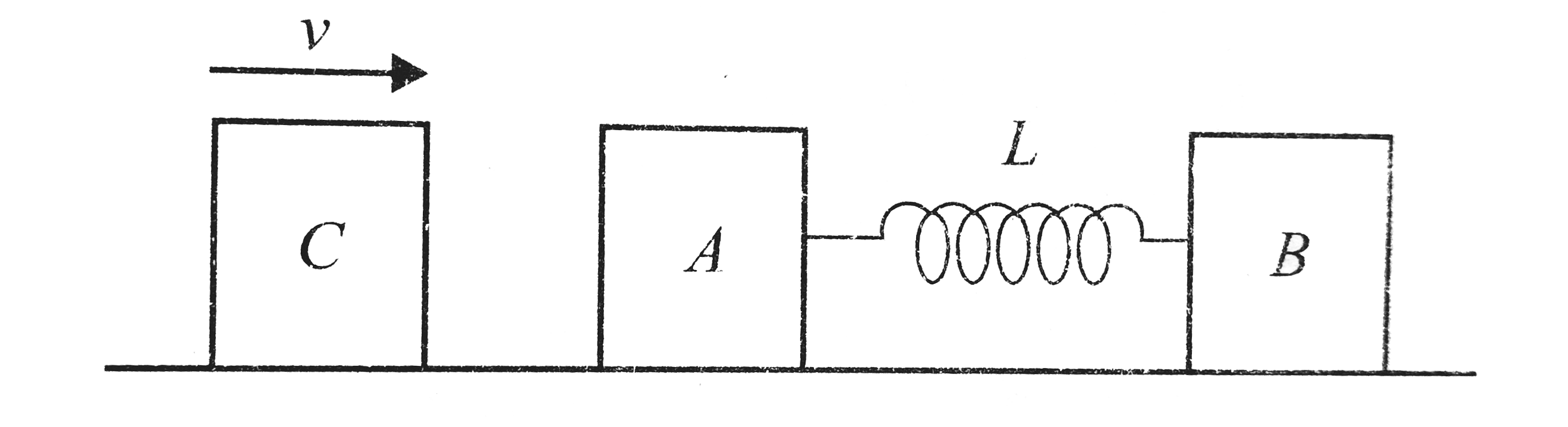
View Solutionm द्रव्यमान के दो ब्लॉक A तथा B एक स्प्रिंग द्वारा जुड़े हैं। स्प्रिंग की वास्तविक लम्वाई L तथा स्प्रिंग नियतांक k है । प्रारम्भ में ब्लॉक एक चिकने क्षैतिज फर्श पर स्प्रिंग की स्वाभाविक लम्बाई के साथ चित्रानुसार विरामावस्था में हैं। A तथा B के समान ही m द्रव्यमान का एक अन्य ब्लॉक C, A तथा B को मिलाने वाली रेखा के अनुदिश v चाल से फर्श पर गति करता है तथा A से प्रत्यास्थ संघट्ट करता है, तब
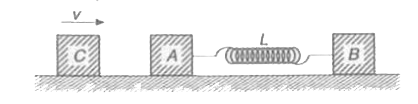
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View Solution
