Two identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
1:1
1:2
1:3
1:4
The correct Answer is:D
To solve the problem of finding the ratio of equivalent capacitance when two identical capacitors are connected in series and then in parallel, we can follow these steps:
Step 1: Define the Capacitance of Each Capacitor
Let the capacitance of each identical capacitor be C.
Step 2: Calculate the Equivalent Capacitance for Series Connection
When two capacitors are connected in series, the formula for the equivalent capacitance Ceq,series is given by:
1Ceq,series=1C1+1C2
Since both capacitors have the same capacitance C:
1Ceq,series=1C+1C=2C
Thus, the equivalent capacitance for the series connection is:
Ceq,series=C2
Step 3: Calculate the Equivalent Capacitance for Parallel Connection
When the same two capacitors are connected in parallel, the formula for the equivalent capacitance Ceq,parallel is:
Ceq,parallel=C1+C2
Again, since both capacitors have the same capacitance C:
Ceq,parallel=C+C=2C
Step 4: Find the Ratio of Equivalent Capacitances
Now, we need to find the ratio of the equivalent capacitance in series to that in parallel:
Ratio=Ceq,seriesCeq,parallel=C22C
Simplifying this gives:
Ratio=C2⋅12C=14
Step 5: Express the Ratio
The ratio of the equivalent capacitance when the capacitors are in series to when they are in parallel is:
Ratio=1:4
Thus, the final answer is that the ratio of equivalent capacitance of capacitors in series to that in parallel is 1:4.
---
Let the capacitance of each identical capacitor be C.
When two capacitors are connected in series, the formula for the equivalent capacitance Ceq,series is given by:
When the same two capacitors are connected in parallel, the formula for the equivalent capacitance Ceq,parallel is:
Now, we need to find the ratio of the equivalent capacitance in series to that in parallel:
The ratio of the equivalent capacitance when the capacitors are in series to when they are in parallel is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
View SolutionIn, identical capacitors are connected in the following three configurations.
 .
.
The ratio of the total capacitances in (i),(ii), and (iii), respectively, is .
View Solutionn equal resistors are first connected in series and then connected in parallel. What is the ratio of the maximum to the minimum resistance ?
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
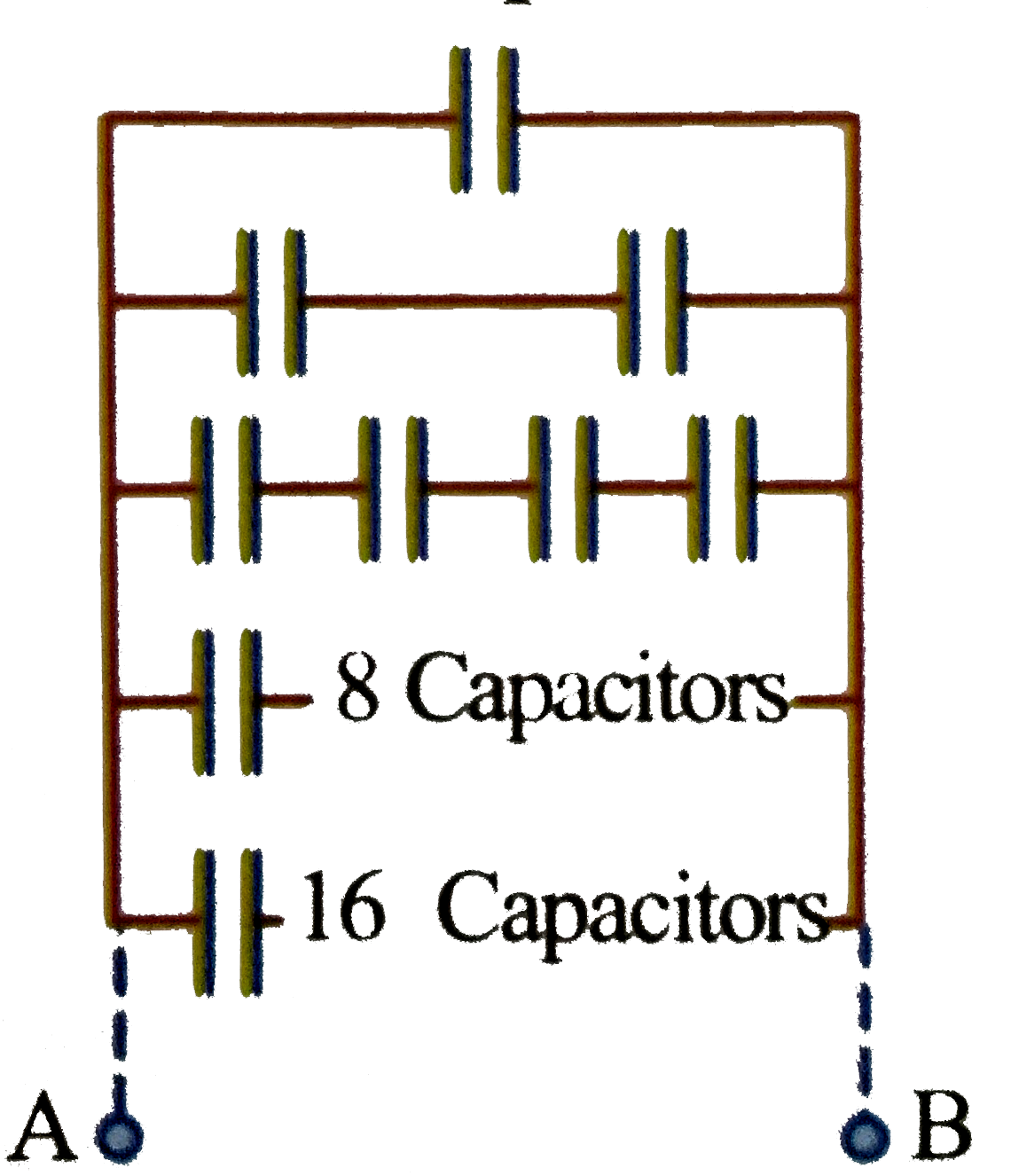 .
.
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
 .
.
View SolutionFour capacitors of each of capacity 3μF are connected as shown in the adjoining figure. The ratio of equivalent capacitance between A and B and between A and C will be

View SolutionTwo conducting wires of the same material and of equal length and equal diameters are first connected in series and then in parallel in an electric circuit. The ratio of the heat produced in series and parallel combinations would be :
View SolutionFour capacitors are connected as shown in the figure. The equivalent capacitance between P and Q is
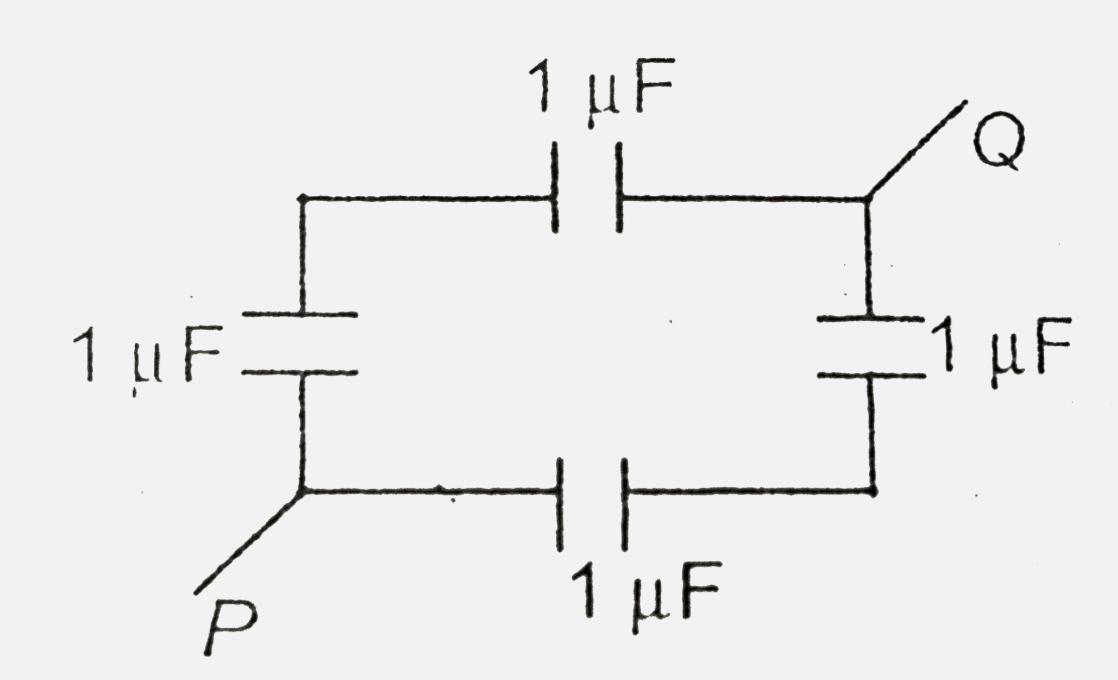
View SolutionThere are 7 identical capacitors. The equivalent capacitance when they are connected in series is C. The equivalent capacitance when they are connected in parallel is
View Solution
