Two identical charged particles are projected simul- taneously from origin in xy plane. Each particle has charge q and mass m and has been projected with velocity v as shown in the figure. There exists a uniform magnetic field B in negative z direction.
(i) Find −−→V1.−−→V2at time t where −−→V1and−−→V2 are velocities of the particles at time t.
Find −−→V1.−−→V2 at time t=πmqB where −−→r1.−−→V2are the position vectors of the two particles.
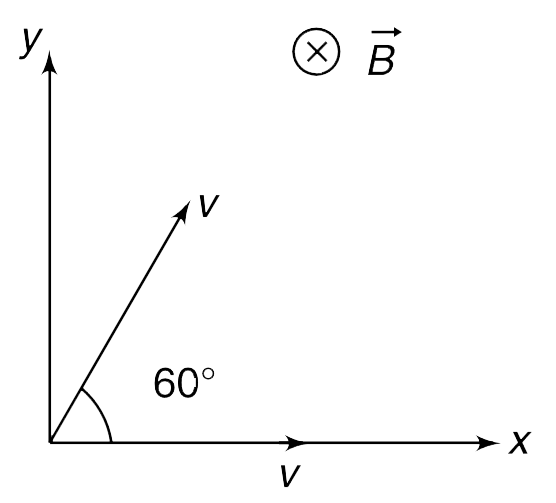
The correct Answer is:(i)V22" "(ii) 2((mv)/(qB))^(2)
Step by step video, text & image solution for Two identical charged particles are projected simul- taneously from origin in xy plane. Each particle has charge q and mass m and has been projected with velocity v as shown in the figure. There exists a uniform magnetic field B in negative z direction. (i) Find underset(V)to_(1).underset(V)to_(2)at time t where underset(V)to_(1) and underset(V)to_(2) are velocities of the particles at time t. Find underset(V)to_(1).underset(V)to_(2) at time t=(pim)/(qB) where underset(r)to_(1).underset(V)to_(2)are the position vectors of the two particles. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-2
13 Videos
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-3
4 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
- NUCLEAR PHYSICSBOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions
54 Videos
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
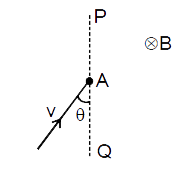
time spent
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
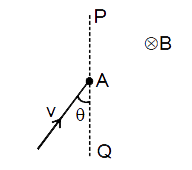
impulse of magnetic force.
View Solution
Knowledge Check
A charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
Amv0qBB2mv0qBCmv02qBDNone of theseA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.
 AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B.
AMagnetic field at P is μ0i4πr[2+√2]⊙BThe magnetic field at P is μ0i/2πr.CThe particle initially accelerated towards wire A.DThe particle initially accelerated towards wire B.A particle of charge q and mass m, is fired perpenducular to a magnetic field (B) with a velocity v. What is the frequency of revolution of the particle?
A2πBqB2πBqmC2πmBqDBq2πm
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA particle of mass m and charge q is moving in a region where uniform electric field −−→E and and uniform mag-netic field −−→Bare present. It is given that −−→E∣∣→E∣∣=−−→B∣∣→B∣∣. At time t = 0, velocity of the particle is −−→V0 and −−→V0.−−→E=0. Write the velocity of the particle at time t.
View SolutionTwo particles having identical masses and charges 2Q and Q are moving with velocities v and 2v resp. In uniform magnetic field B. Find ratio of radius of circle described by them
View SolutionA particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=πm2qB.
View SolutionA particle of mass m and charge q is projected into a uniform magnetic field −−→B=−B0ˆK with velocity −−→V−V0ˆi from origin. The position vector of the particle at time t is −−→r. Find the impulse of magnetic force on the particle by the time −−→r.−−→V becomes zero for the first time.
View Solution
