Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
20
22
24
26
The correct Answer is:a
To solve the problem, we need to determine the number of points on the circumference of a circle where the intensity of the interference pattern produced by two coherent sources is at a maximum. The sources are separated by a distance x=5λ, where λ is the wavelength of the emitted waves.
1. Understanding the Setup:
- We have two coherent sources S1 and S2 placed on the diameter of a circle of radius R.
- The separation between the sources is x=5λ.
2. Identifying Maximum Intensity Conditions:
- Maximum intensity occurs when the path difference between the waves from the two sources at any point on the circle is an integer multiple of the wavelength λ.
- Mathematically, this can be expressed as:
Δx=S1P−S2P=nλ
where n is any integer (0, ±1, ±2, ±3, ...).
3. Calculating Maximum Path Difference:
- The maximum path difference occurs when the distance between the two sources is equal to the separation x.
- Given that x=5λ, the maximum path difference Δx can take values from −5λ to 5λ.
4. Finding Possible Values of n:
- The integer values of n that satisfy the condition −5λ≤nλ≤5λ are:
n=−5,−4,−3,−2,−1,0,1,2,3,4,5
- This gives us a total of 11 possible values for n.
5. Counting the Maxima:
- Each integer value of n corresponds to a point of maximum intensity on the circle.
- Therefore, the total number of points on the circle where the intensity is maximum is 11.
Final Answer:
The number of points on the circle of maximum intensity is 11.
- We have two coherent sources S1 and S2 placed on the diameter of a circle of radius R.
- The separation between the sources is x=5λ.
- Maximum intensity occurs when the path difference between the waves from the two sources at any point on the circle is an integer multiple of the wavelength λ.
- Mathematically, this can be expressed as:
Δx=S1P−S2P=nλ
where n is any integer (0, ±1, ±2, ±3, ...).
- The maximum path difference occurs when the distance between the two sources is equal to the separation x.
- Given that x=5λ, the maximum path difference Δx can take values from −5λ to 5λ.
- The integer values of n that satisfy the condition −5λ≤nλ≤5λ are:
n=−5,−4,−3,−2,−1,0,1,2,3,4,5
- This gives us a total of 11 possible values for n.
- Each integer value of n corresponds to a point of maximum intensity on the circle.
- Therefore, the total number of points on the circle where the intensity is maximum is 11.
The number of points on the circle of maximum intensity is 11.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Knowledge Check
Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=nλ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
A2n+1B4nC4n−2D4n+2Two sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
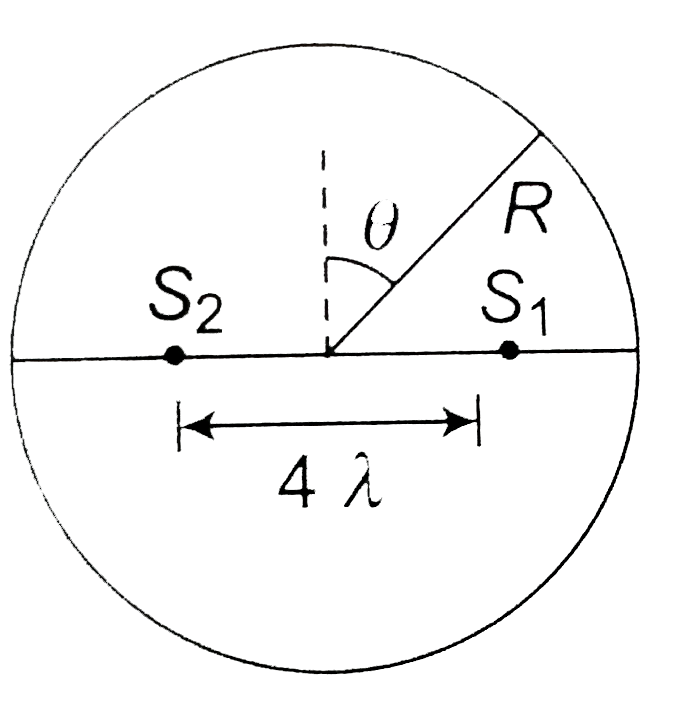 A12B16C4D20
A12B16C4D20If two coherent source are placed at a distance 3λ from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?
 A16B12C8D4
A16B12C8D4
Two coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
View SolutionIf the equations of the two diameters of a circle are x−y=5 and 2x+y=4 and the radius of the circle is 5, find the equation of the circle.
View SolutionLet PQandRS be tangent at the extremities of the diameter PR of a circle of radius r. If PSandRQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQxRS .
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View Solution
