Two identical conducting wires AOBandCOD are placed at right angles to each other. The wire AOB carries an electric current I1andCOD carries a current I2. The magnetic field on a point lying at a distance d from O, in a direction perpendicular to the plane of the wires AOBandCOD, will be given by
μ02πd(I1I2)
μ02πd(I1+I2)
μ02πd(I21−I22)
μ02πd(I21+I22)1/2
The correct Answer is:d
To find the magnetic field at a point P, which is at a distance d from the intersection point O of two perpendicular wires AOB and COD carrying currents I1 and I2 respectively, we can follow these steps:
Step 1: Understand the Configuration
We have two identical conducting wires:
- Wire AOB carries current I1.
- Wire COD carries current I2.
These wires are placed at right angles to each other.
Step 2: Calculate the Magnetic Field due to Wire AOB
The magnetic field (B1) at a distance d from a long straight wire carrying current I can be calculated using the formula:
B=μ0I2πr
where:
- μ0 is the permeability of free space,
- I is the current through the wire,
- r is the distance from the wire.
For wire AOB, the distance from point O to point P is d, so:
B1=μ0I12πd
Step 3: Calculate the Magnetic Field due to Wire COD
Similarly, for wire COD, the magnetic field (B2) at the same distance d is given by:
B2=μ0I22πd
Step 4: Determine the Direction of the Magnetic Fields
Using the right-hand rule:
- The magnetic field B1 due to wire AOB will be directed out of the plane (let's say in the positive z-direction).
- The magnetic field B2 due to wire COD will be directed into the plane (let's say in the negative z-direction).
Step 5: Calculate the Resultant Magnetic Field
Since the two magnetic fields are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field (B):
B=√B21+B22
Substituting the values of B1 and B2:
B=√(μ0I12πd)2+(μ0I22πd)2
Step 6: Simplify the Expression
Factoring out common terms:
B=μ02πd√I21+I22
Final Answer
Thus, the magnetic field at point P is given by:
B=μ02πd√I21+I22
We have two identical conducting wires:
- Wire AOB carries current I1.
- Wire COD carries current I2.
These wires are placed at right angles to each other.
The magnetic field (B1) at a distance d from a long straight wire carrying current I can be calculated using the formula:
B=μ0I2πr
where:
- μ0 is the permeability of free space,
- I is the current through the wire,
- r is the distance from the wire.
B1=μ0I12πd
Similarly, for wire COD, the magnetic field (B2) at the same distance d is given by:
B2=μ0I22πd
Using the right-hand rule:
- The magnetic field B1 due to wire AOB will be directed out of the plane (let's say in the positive z-direction).
- The magnetic field B2 due to wire COD will be directed into the plane (let's say in the negative z-direction).
Since the two magnetic fields are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field (B):
B=√B21+B22
Substituting the values of B1 and B2:
B=√(μ0I12πd)2+(μ0I22πd)2
Factoring out common terms:
B=μ02πd√I21+I22
Thus, the magnetic field at point P is given by:
B=μ02πd√I21+I22
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
Two identical long conducting wires AOB and COD are placed at right angle to each other, with one above other such that O is their common point for the two. The wires carry l1 and l2 currents, respectively. Point P is lying at distance d from 0 along a direction perpendicular to the plane containing the wire. The magnetic field at the point P will be
View SolutionA conducting wire carries 5A current. Its lenghts 6cm. Then the magnitic field intensity at a distance of 4cm from the wire on the perpendicular bisector of the wire is
_2019_CBT8_E01_002_Q01.png)
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
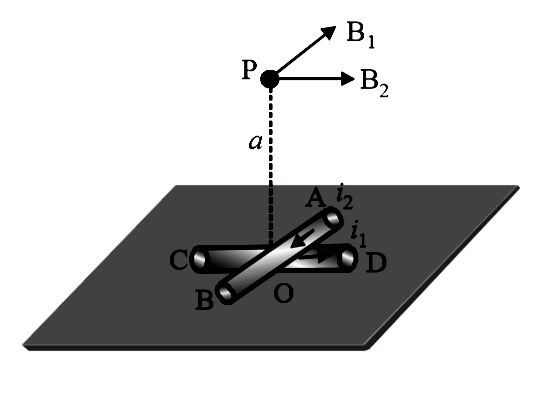
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is

View SolutionMagnetic field at a distance a from long current carrying wire is proportional to
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is

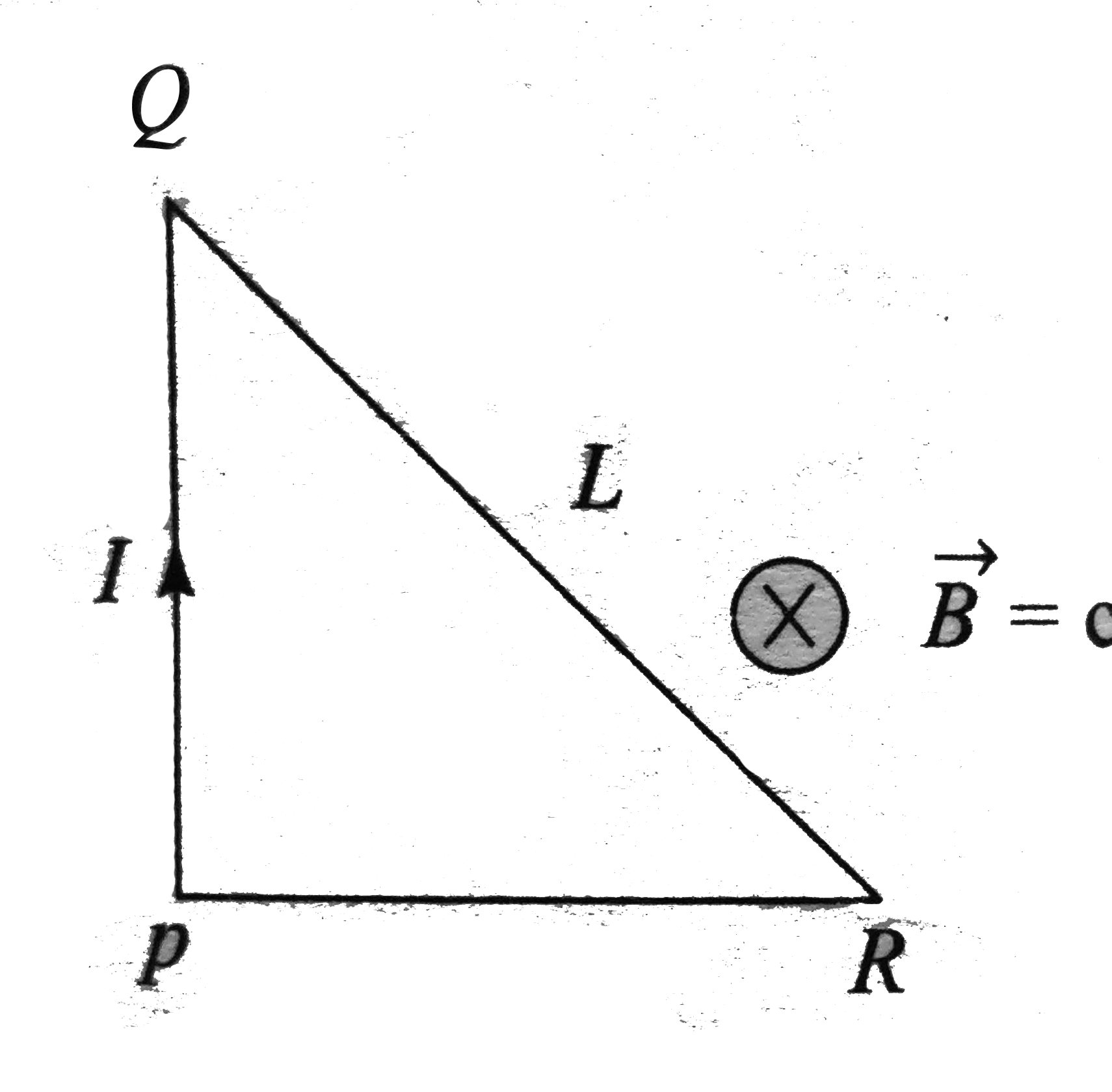
View SolutionThe rigid conducting thin wire frame carries an electric current I and this frame is inside a uniform magnetic field →B as shown in Fig. 1.146. Then,
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View SolutionA wire carries an alternating current i=i0sinωt. In there an electric field in the vicinity of the wire?
View SolutionA very long wire carrying a current I=5.0A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the Point of bending at a distance l=35cm from it.
View Solution
