When a proton is released from rest in a room, it starts with an initial acceleration a0 towards west. When it is projected towards north with a speed v0 it moves with an initial accelaration 3a0 towards west. The electric and the maximum possible magnetic field in the room
(i) ma0e, towards west
(ii) 2ma0ev0, downward
(iii) ma0e, towards east
(iv) 2ma0ev0, upward
ma0ewest2ma0ev0up
ma0ewest2ma0ev0down
ma0eeast3ma0ev0up
ma0eeast3ma0ev0down
The correct Answer is:b
To solve the problem, we will analyze the two scenarios provided in the question step by step.
Step 1: Analyze the first scenario
When the proton is released from rest, it experiences an initial acceleration a0 towards the west. Since the proton is positively charged, it will accelerate in the direction of the electric field.
1. Force on the proton: The force acting on the proton can be expressed as:
F=ma0
where m is the mass of the proton.
2. Electric field: The force due to the electric field can be expressed as:
F=qE
where q is the charge of the proton and E is the electric field.
3. Setting the forces equal: Since both forces are acting on the proton, we can set them equal:
ma0=qE
4. Solving for the electric field: Rearranging gives us:
E=ma0q
Since the charge of the proton q is denoted as e, we can write:
E=ma0e
The direction of the electric field is towards the west.
Step 2: Analyze the second scenario
In the second scenario, the proton is projected towards the north with a speed v0 and experiences an acceleration of 3a0 towards the west.
1. Net force on the proton: The net force acting on the proton can be expressed as:
Fnet=m(3a0)
2. Forces acting on the proton: In this case, the forces acting on the proton are due to both the electric field and the magnetic field. The magnetic force can be expressed as:
FB=q(v0×B)
Since the angle between the velocity v0 (north) and the magnetic field B is 90 degrees, we can simplify this to:
FB=qv0B
3. Setting up the equation for forces: The total force acting on the proton can be expressed as:
Fnet=FE+FB
Substituting the expressions for the forces gives:
m(3a0)=ma0+qv0B
4. Rearranging the equation: We can rearrange this to find the magnetic field B:
m(3a0)−ma0=qv0B
2ma0=qv0B
5. Solving for the magnetic field: Rearranging gives:
B=2ma0qv0
Substituting q with e (the charge of the proton):
B=2ma0ev0
Step 3: Determine the direction of the magnetic field
Using the right-hand rule, we can determine the direction of the magnetic field. The velocity is towards the north, and the net force (due to acceleration) is towards the west. Therefore, the magnetic field must be directed downward.
Conclusion
From the analysis, we find:
1. The electric field E is given by:
E=ma0e(towards west)
2. The magnetic field B is given by:
B=2ma0ev0(downward)
Final Answers:
- The electric field is ma0e towards west (Option i).
- The magnetic field is 2ma0ev0 downward (Option ii).
When the proton is released from rest, it experiences an initial acceleration a0 towards the west. Since the proton is positively charged, it will accelerate in the direction of the electric field.
F=ma0
where m is the mass of the proton.
F=qE
where q is the charge of the proton and E is the electric field.
ma0=qE
E=ma0q
Since the charge of the proton q is denoted as e, we can write:
E=ma0e
The direction of the electric field is towards the west.
In the second scenario, the proton is projected towards the north with a speed v0 and experiences an acceleration of 3a0 towards the west.
Fnet=m(3a0)
FB=q(v0×B)
Since the angle between the velocity v0 (north) and the magnetic field B is 90 degrees, we can simplify this to:
FB=qv0B
Fnet=FE+FB
Substituting the expressions for the forces gives:
m(3a0)=ma0+qv0B
m(3a0)−ma0=qv0B
2ma0=qv0B
B=2ma0qv0
Substituting q with e (the charge of the proton):
B=2ma0ev0
Using the right-hand rule, we can determine the direction of the magnetic field. The velocity is towards the north, and the net force (due to acceleration) is towards the west. Therefore, the magnetic field must be directed downward.
From the analysis, we find:
1. The electric field E is given by:
E=ma0e(towards west)
2. The magnetic field B is given by:
B=2ma0ev0(downward)
- The electric field is ma0e towards west (Option i).
- The magnetic field is 2ma0ev0 downward (Option ii).
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
when a proton is released from rest in a room, it starts with an initial acceleration a0 towards west . When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the elecrtic field and the minimum possible magnetic field in the room.
View SolutionWhen a proton is released from rest in a room, it starts with an initial acceleration a0 towards west. When it is projected towards north with a speed v0 it moves with an initial acceleration 3a0 towards west. The electric and magnetic fields in the room are
View SolutionCalculate the relative acceleration of A w.r.t. B if B is moving with acceleration a0 towards right.

View SolutionA particle has a velocity u towards east at t=0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacement in the first 10 seconds and the next 10 seconds:
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
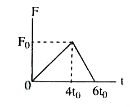
Maximum force exerted by the bat on the ball is
View SolutionA particle has a velocity u towards east at t=0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionWhen proton of KE = 1.0 MeV moving in South to North direction enters the magnetic field (from West to East direction), it accelerates with a=1012ms2 . The magnitude of magnetic field is-
View SolutionWhen proton of KE = 1.0 MeV moving in South to North direction enters the magnetic field (from West to East direction), it accelerates with a=1012ms2 . The magnitude of magnetic field is-
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
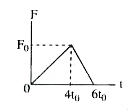
Average force exerted by the bat on the ball is
View Solution
